Геометрическая прогрессия.

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.

Таким образом, геометрическая прогрессия – это числовая последовательность { b_n }, заданная рекуррентно соотношениями

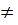b ₁ = b, b_n = b_{n –1} q (n = 2, 3, 4…). (b и q – заданные числа, b 0, q 0).

Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b₁ = 2, q = 3.

Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b₁ = 2, q = –1.

Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b₁ = 8, q = 1.

Геометрическая прогрессия является возрастающей последовательностью, если b ₁> 0, q > 1, и убывающей, если b ₁> 0, 0 < q < 1.

Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е. b ₁², b ₂², b ₃², …, b_n ²,… является геометрической прогрессией, первый член которой равен b ₁², а знаменатель – q ².

Формула n- го члена геометрической прогрессии имеет вид

b_n = b ₁ q^{n– 1}.

Можно получить формулу суммы членов конечной геометрической прогрессии.

Пусть дана конечная геометрическая прогрессия

b ₁, b ₂, b ₃, …, b_n а S_n – сумма ее членов, т.е. S_n = b ₁ + b ₂+ b ₃ + … + b_n.

Принимается, что q 1. Для определения S_n применяется искусственный прием: выполняются некоторые геометрические преобразования выражения S_nq.

Тогда

S_nq = (b ₁ + b ₂ + b ₃+ … + b_{n –1} + b_n) q = b ₂ + b ₃ + b ₄ + …+ b_n + b_nq = S_n + b_nq – b ₁.

Таким образом, S_nq = S_n + b_nq – b ₁ и, следовательно,

.

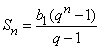Это формула с уммы n членов геометрической прогрессии для случая, когда q 1.

При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае S_n = b₁ n.

Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов. Действительно, так как

b_n= b_{n- 1} q;

b_n= b_{n+ 1} /q,

следовательно, b_n ² = b_{n– 1} b_{n+ 1} и верна следующаятеорема(характеристическое свойство геометрической прогрессии):

числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.

Не нашли, что искали? Воспользуйтесь поиском: