Заметьте, центр распределения сдвинулся при изменении параметра .

28. Вероятность попадания на отрезок.

Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал , равна ,

Где , .

□ Учитывая, что вероятность есть приращение функции распределения на отрезке и учитывая формулу получим:

. ■

29. Правило "трех сигм".

Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину (по абсолютной величине), равна, где.

□ . Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим

. ■

«правило трех сигм»:

Если случайная величина Х имеет нормальный закон распределения с параметрами а и , т.е. N(a; ), то практически достоверно, что ее значения заключены в интервале ().

Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на (по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала:

.

30. Системы случайных величин.

Существуют случайные величины, которые определяются двумя, тремя и т.д. числами. Такие случайные величины называются двумерными, трехмерными и т.д.

В зависимости от типа, входящих в систему случайных величин, системы могут быть дискретными, непрерывными или смешанными, если в систему входят различные типы случайных величин.

Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.

31. Законы распределения системы двух случайных величин.

Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.

Свойства функции распределения системы двух случайных величин:

1) Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.

2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.

3) При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю.

4) Функция распределения является неубывающей функцией по каждому аргументу.

5) Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:

32. Условные законы распределения.

Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.

Условная плотность распределения вычисляется по формулам:

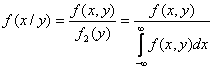
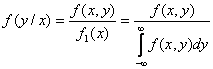
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.

33. Зависимые и независимые случайные величины.

При изучении систем случайных величин всегда следует обращать внимание на степень и характер их зависимости. Эта зависимость может быть более или менее ярко выраженной, более или менее тесной. В некоторых случаях зависимость между случайными величинами может быть настолько тесной, что, зная значение одной случайной величины, можно в точности указать значение другой. В другом крайнем случае зависимость между случайными величинами является настолько слабой и отдаленной, что их можно практически считать независимыми.

Случайная величина называется независимой от случайной величины , если закон распределения величины не зависит от того, какое значение приняла величина .

Для непрерывных случайных величин условие независимости от может быть записано в виде:

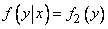
при любом .

Напротив, в случае, если зависит от , то

.

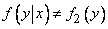Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.

Случайные величины и называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины и называются зависимыми.

Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:

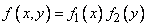, (8.5.2)

т. е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.

Условие (8.5.2) может рассматриваться как необходимое и достаточное условие независимости случайных величин.

Часто по самому виду функции 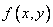можно заключить, что случайные величины , являются независимыми, а именно, если плотность распределения 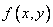распадается на произведение двух функций, из которых одна зависит только от 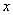, другая - только от , то случайные величины независимы.

Изложенный критерий суждения о зависимости или независимости случайных величин исходит из предположения, что закон распределения системы нам известен. На практике чаще бывает наоборот: закон распределения системы 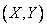не известен; известны только законы распределения отдельных величин, входящих в систему, и имеются основания считать, что величины и независимы. Тогда можно написать плотность распределения системы как произведение плотностей распределения отдельных величин, входящих в систему.

Остановимся несколько подробнее на важных понятиях о «зависимости» и «независимости» случайных величин.

Понятие «независимости» случайных величин, которым мы пользуемся в теории вероятностей, несколько отличается от обычного понятия «зависимости» величин, которым мы оперируем в математике. Действительно, обычно под «зависимостью» величин подразумевают только один тип зависимости - полную, жесткую, так называемую - функциональную зависимость. Две величины и называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.

В теории вероятностей мы встречаемся с другим, более общим, типом зависимости — с вероятностной или «стохастической» зависимостью. Если величина связана с величиной вероятностной зависимостью, то, зная значение , нельзя указать точно значение , а можно указать только ее закон распределения, зависящий от того, какое значение приняла величина .

Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Таким образом, функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай - полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости - от самой сильной до самой слабой. Те физические величины, которые на практике мы считаем функционально зависимыми, в действительности связаны весьма тесной вероятностной зависимостью: при заданном значении одной из этих величин другая колеблется в столь узких пределах, что ее практически можно считать вполне определенной. С другой стороны, те величины, которые мы на практике считаем независимыми, и действительности часто находятся в некоторой взаимной зависимости, но эта зависимость настолько слаба, что ею для практических целей можно пренебречь.

Вероятностная зависимость между случайными величинами очень часто встречается на практике. Если случайные величины и находятся в вероятностной зависимости, это не означает, что с изменением величины величина изменяется вполне определенным образом; это лишь означает, что с изменением величины величина имеет тенденцию также изменяться (например, возрастать или убывать при возрастании ). Эта тенденция соблюдается лишь «в среднем», в общих чертах, и в каждом отдельном случае от нее возможны отступлении.

34. Числовые характеристики системы двух случайных величин.

Первые начальные моменты представляют собой математические ожидание величин Х и У, входящих в систему:

a_1,0 (x, y) = m_x; a_0,1 (x, y) = m_y. (11.5)

Совокупность математических ожиданий представляет собой характеристику положения системы. Геометрически это координаты средней точки на плоскости, вокруг которой происходит рассеивание случайных точек (Х,У).

m_1,0 (x, y) = М[ Х - m_x ]=0 m_0,1 (x, y)= М[ Y - m_y)=0; (11.6)

a_2,0 (x, y) = a₂ (x) a_0,2 (x, y) = a₂ (y)

На практике широко используются вторые центральные моменты системы. Два из них представляют собой дисперсии, которые характеризуют рассеивание случайной точки в направлении осей 0 Х и 0 Y:

m_2,0 (x, y) = М[ Х - m_x)²=D[X]= D _x; m_0,2 (x, y) = М[ Y - m_y)² ]=D[ Y ]= D_y; (11.7)

Не нашли, что искали? Воспользуйтесь поиском: