
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ковариация, коэффициент корреляции.
Особую роль играет центральный момент порядка 1+1 или второй смешанный центральный момент, который называется ковариацией или корреляционным моментом
m1,1 (x, y) = Kxy=  (11.8)
(11.8)
Ковариация представляет собой математическое ожидание произведения центрированных случайных величин X и Y и характеризует степень линейной статистической зависимости величин X и Y и рассеивание относительно точки (mx, my):
Kxy =  , (11.9)
, (11.9)
Или

 (11.10)
(11.10)
Расчетные формулы для определения ковариации:
 (11.11)
(11.11)
Свойства корреляции:
1. Kxy=Kyx.
2. Корреляционный момент двух независимых случайных величин Х и У равен нулю.
3. Абсолютная величина корреляционного момента двух случайных величин не превышает среднего геометрического их дисперсий
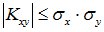 или
или 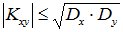
Если  , случайные величины Х и Y называются коррелированными. Если
, случайные величины Х и Y называются коррелированными. Если 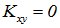 , то необязательно, что Х и Y независимы. В этом случае они называются некоррелированными. Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает их коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.
, то необязательно, что Х и Y независимы. В этом случае они называются некоррелированными. Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает их коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.
Величина ковариации зависит единиц измерения каждой из случайных величин, входящих в систему и от того, насколько каждая из случайных величин отклоняется от своего математического ожидания (одна – мало, вторая – сильно, все равно  будет мал).
будет мал).
Поэтому для характеристики связи между Х и Y в чистом виде переходят к безразмерной характеристике, которая называется Коэффициент корреляции rxy характеризует степень линейной зависимости величин:
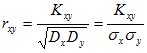 (11.12)
(11.12)
Свойства коэффициента корреляции:
1. Абсолютная величина коэффициента корреляции двух случайных величин не превышает единицы: 
2. │rxy│=1 если Y=aХ+b
Коэффициент корреляции служит для оценки тесноты линейной связи между Х и Y: чем ближе абсолютная величина коэффициента корреляции к 1, тем связь сильнее, чем ближе к 0, тем слабее.
3. Если величины X и Y независимы, то rxy = 0.
35. Регрессия
Регрессия - величина, выражающая зависимость среднего значения случайной величины у от значений случайной величины х.
Уравнение регрессии выражает среднюю величину одного признака как функцию другого.
Функция регрессии - это модель вида у = х», где у - зависимая переменная (результативный признак); х - независимая, или объясняющая, переменная (признак-фактор).
Линия регрессии - график функции у = f (x).
2 типа взаимосвязей между х и у:
1) может быть неизвестно, какая из двух переменных является независимой, а какая - зависимой, переменные равноправны, это взаимосвязь корреляционного типа;
2) если х и у неравноправны и одна из них рассматривается как объясняющая (независимая) переменная, а другая - как зависимая, то это взаимосвязь регрессионного типа.
Виды регрессий:
1) гиперболическая - регрессия равносторонней гиперболы: у = а + b / х + Е;
2) линейная - регрессия, применяемая в статистике в виде четкой экономической интерпретации ее параметров: у = а+b*х+Е;
3) логарифмически линейная - регрессия вида: In у = In а + b * In x + In E
4) множественная - регрессия между переменными у и х1, х2... xm, т. е. модель вида: у = f(х1, х2... xm)+E, где у - зависимая переменная (результативный признак), х1, х2... xm - независимые, объясняющие переменные (признаки-факторы), Е- возмущение или стохастическая переменная, включающая влияние неучтенных факторов в модели;
5) нелинейная - регрессия, нелинейная относительно включенных в анализ объясняющих переменных, но линейная по оцениваемым параметрам; или регрессия, нелинейная по оцениваемым параметрам.
6) обратная - регрессия, приводимая к линейному виду, реализованная в стандартных пакетах прикладных программ вида: у = 1/a + b*х+Е;
7) парная - регрессия между двумя переменными у и x, т. е, модель вида: у = f (x) + Е, где у -зависимая переменная (результативный признак), x – независимая, объясняющая переменная (признак - фактор), Е - возмущение, или стохастическая переменная, включающая влияние неучтенных факторов в модели.
36. Коэффициент корреляции.
Корреляция - величина, отражающая наличие связи между явлениями, процессами и характеризующими их показателями.
Корреляционная зависимость - определение зависимости средней величины одного признака от изменения значения другого признака.
Коэффициент корреляции величин х и у (rxy) свидетельствует о наличии или отсутствии линейной связи между переменными:

где 
 (-1; 1). Если:
(-1; 1). Если:  = -1, то наблюдается строгая отрицательная связь;
= -1, то наблюдается строгая отрицательная связь;  = 1, то наблюдается строгая положительная связь;
= 1, то наблюдается строгая положительная связь;  = 0, то линейная связь отсутствует.
= 0, то линейная связь отсутствует.
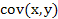 - ковариация, т. е. среднее произведение отклонений признаков от их средних квадратических отклонений.
- ковариация, т. е. среднее произведение отклонений признаков от их средних квадратических отклонений.
Коэффициент корреляции может служить мерой зависимости случайных величин.
Корреляция для нелинейной регрессии:
 при R
при R  [0;1].
[0;1].
Чем ближе R к 1, тем теснее связь рассматриваемых признаков.
37. Двумерная нормальная случайная величина.
Двумерной случайной величино й называют систему из двух случайных величин  , для которой определена вероятность
, для которой определена вероятность 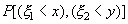 совместного выполнения неравенств
совместного выполнения неравенств  и
и  , где x и y - любые действительные числа.
, где x и y - любые действительные числа.
Функция двух переменных

| (34) |
определенная для любых x и y, называется функцией распределения системы двух случайных величин 
Будем рассматривать  и
и  как декартовы координаты точки на плоскости. Точка
как декартовы координаты точки на плоскости. Точка  может занимать то или иное положение на плоскости
может занимать то или иное положение на плоскости 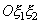 . Тогда функция распределения даст вероятность того, что случайная точка
. Тогда функция распределения даст вероятность того, что случайная точка  попадает в область
попадает в область  , изображенную на рис. 13.
, изображенную на рис. 13.

Двумерная случайная величина  называется дискретной, если
называется дискретной, если  и
и  - дискретные величины.
- дискретные величины.
Пусть возможные значения  и
и  образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины
образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины  имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что
имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что 

Функция распределения F(х, у) имеет вид

где двойная сумма распространена на те i и j, для которых xi<x и yj<y.
Двумерную случайную величину  так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины
так же, как и одномерную, можно задавать таблицей. Первая строка таблицы содержит возможные значения случайной величины  , а первый столбец — возможные значения
, а первый столбец — возможные значения  . В остальных клетках таблицы указаны соответствующие вероятности, причем их сумма всегда равна единице.
. В остальных клетках таблицы указаны соответствующие вероятности, причем их сумма всегда равна единице.
38. Законы больших чисел.
Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.
Всегда найдётся такое конечное число испытаний, при котором с любой заданной наперёд вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.
Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.
На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.
Не нашли, что искали? Воспользуйтесь поиском: