ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пстроение экономико - математических моделей задач линейного программирования
СОДЕРЖАНИЕ
| Введение | ||
| §1. | Линейное программирование. Сущность линейного программирования | 5-13 |
| §2. | Геометрический метод решения задач линейного программирования | 13-16 |
| §3. | Симплексный метод решения задач | 16-27 |
| §4. | Транспортная задача | 27-39 |
Введение
Среди задач математического программирования лучше всего изученными являются так называемые задачи линейного программирования. Это задачи, в которых целевая функция является линейной функцией независимых переменных, и условия, определяющие допустимые значения этих переменных, имеют вид линейных уравнений или линейных неравенств.
Задачи линейного программирования являются математическими моделями многочисленных задач технико-экономического содержания. Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с поиском способов оптимального распределения и использования ограниченных ресурсов, управления и планирования производственных процессов и т.д.
Целью настоящей работы является знакомство с методами оптимизации, приобретение навыков по решению задач линейного программирования.
Учебно - методическое пособие адресовано студентам всех специальностей СПО по разделу «Линейное программирование».
§ 1. Линейное программирование. Сущность линейного программирования
Линейное программирование есть совокупность математических методов нахождения минимальных и максимальных значений линейных функций в области неотрицательных значений переменных величин при ограничениях, заданных системой линейных уравнений или неравенств.
Определение. Линейная функция вида:
(1)
максимум или минимум, которой находится в задаче линейного программирования, называется целевой функцией.
Задачей линейного программирования называется задача вида:
Найти 
целевой функции (1) при условии, что на переменные 
наложены ограничения в виде линейных равенств или неравенств:
(2)
Искомые переменные могут выражать: объемы производства различных видов продукции, планируемые под сельскохозяйственные культуры, посевные площади, количество составляющих веществ в различных смесях, количество единиц приобретаемого продукта и т.д. Функция 
может представлять собой стоимость выпускаемой продукции, ожидаемый урожай, доход, ущерб, а условия ограничений, которым подчинены 
, отражают ограниченность имеющихся естественных материальных, денежных ресурсов, требования к количеству продукции или производственных мощностей.
Определение. Совокупность значений переменных удовлетворяющих условиям задачи линейного программирования и образующих область определения функции , называется областью допустимых значений переменных.
Определение Набор значений из допустимой области, при которой целевая функция (1) принимает наибольшее или наименьшее значения называется решением задачи линейного программирования или оптимальным планом.
Замечание: определение минимального значения целевой функции можно свести к определению максимального значения функции 
, так как 
.
Определение. Критерием оптимальности называется некоторый показатель, имеющий экономическое содержание, служащий формализацией конкретной цели управления и выражаемый при помощи целевой функции. Задача линейного программирования может быть записана в матричной форме:
при ограничениях 
(3)
в координатной форме:
1) , при ограничениях
2) 
3) 
с использованием знака суммирования:
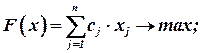при ограничениях
Каноническая модель задачи линейного программирования имеет вид:
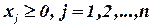. (4)
Математическая модель экономического объекта – это его отображение в виде математических соотношений (функций, уравнений, неравенств, графиков и т.д.).
Алгоритм построения математической модели задачи линейного программирования.
1. Уяснить экономическое содержание задачи.
2. Выбрать переменные задачи.
3. Составить целевую функцию.
4. Составить систему ограничений.
5. Поставить условие не отрицательности на переменные.
Пстроение экономико - математических моделей задач линейного программирования
Не нашли, что искали? Воспользуйтесь поиском: