ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
I. Постановка задачи об использовании ресурсов
Задача 1. Для изготовления 
видов продукции 
предприятие использует 
видов сырья 
. Запасы ресурса 
составляют в 
единиц 
. Известны также технологические коэффициенты 
- число единиц ресурса , затрачиваемого на изготовление единицы продукции 
. Прибыль от реализации единицы продукции равна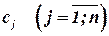 
. Необходимо составить такой план выпуска продукции, при котором прибыль от её реализации была бы максимальной. Составим экономико – математическую модель задачи. Для этого условие задачи для наглядности занесли в таблицу.
Обозначим через 
число единиц продукции , запланированных к выпуску. Для изготовления потребуется.
Таблица 1.
| Вид сырья | Запасы сырья | Технологические коэффициенты | |||||
| 
| 
| 
| … |
| … | 
|
| 
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … | … |
|
| 
| 
| 
| … |
| … | 
|
| … | … | … | … | … | … | … | … |
| 
| 
| 
| … | 
| … | 
|
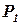
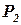
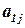
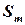
| Прибыль от реализации ед. продукции |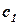 
| 
| … | 
| … | 
| |
| Количество ед. продукции к выпуску | 
| 
| … |
| … | 
|
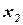
Сырья : 
ед.,
Сырья : 
ед.,
………………………………………………….,
Сырья : 
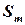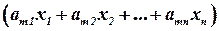ед.
Так как потребление ресурсов не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
(*)
По смыслу задачи 
(**).
Суммарная прибыль 
составит: 
(руб.). (***)
Итак, экономико – математическая модель задачи. Найти такой план выпуска продукции 
, удовлетворяющий системе ограничений (*) и условию неотрицательности (**), при котором функция (***) принимает максимальное значение. Это записывается так:
.
2.Постановка задачи о составлении рациона (задача о диете, задача о смесях)
Задача 2. Имеется видов корма, содержащих питательные вещества . Известно число единиц питательного вещества в единице корма 
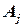(обозначим 
), а также необходимый минимум содержания в рационе питательного вещества , равный 
. Стоимость единицы корма 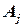равна стоимости корма руб. 
. Необходимо составить рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было не менее установленного предела. Составим экономико – математическую модель задачи.
Обозначим через число единиц корма 
,входящего в рацион. Тогда этот рацион будет включать:
единиц питательного вещества , единиц питательного вещества ,
Таблица 2.
| Питательное вещество | Необходимый минимум питательных веществ | Число единиц питательного вещества в 1 единицу корма | |||||
|
|
| 
| 
| … |
| … | 
|
|
|
|
|
| … |
| … |
|
| … | … | … | … | … | … | … | … |
|
|
|
|
| … |
| … |
|
| … | … | … | … | … | … | … | … |
|
|
|
|
| … |
| … |
|
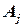
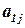
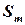
| Стоимость 1 единицы корма |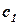
|
| … |
| … |
| |
| Число единиц корма |
|
| … |
| … |
|
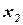
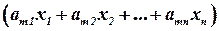единиц питательного вещества .
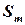Так как содержание питательных веществ должно быть не менее , получим систему неравенств:
(*)
По смыслу задачи (**).
Общая стоимость рациона составит: 
(руб.). (***)
Итак, экономико – математическая модель задачи. Составить рацион , удовлетворяющий системе ограничений (*) и условию неотрицательности (**), при котором функция (***) принимает минимальное значение. Это записывается так: 
.
Не нашли, что искали? Воспользуйтесь поиском: