
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Геометрический метод решения задач линейного программирования
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двухмерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств.
Область допустимых решений задачи строится как пересечение областей решений каждого из заданных ограничений.
Областью решений линейного неравенства 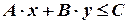 является одна из двух полуплоскостей, на которые прямая
является одна из двух полуплоскостей, на которые прямая  , соответствующая данному неравенству, делит всю координатную плоскость.
, соответствующая данному неравенству, делит всю координатную плоскость.
Для того чтобы определить, какая из двух координатных полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Областью допустимых решений задачи является общая часть полуплоскостей (областей решений всех неравенств системы ограничений) представляющая многогранник.
Теорема. Целевая функция задачи линейного программирования достигает своего экстремального значения в вершинах многогранника решений. Если целевая функция принимает экстремальное значение более чем в одной вершине, то она достигает того же значения в любой точке, лежащей на соединяющем их отрезке.
Задача. Построить область допустимых решений.

Решение. Решим неравенство 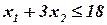 . Построим прямую (границу полуплоскости)
. Построим прямую (границу полуплоскости)  . Определим полуплоскость, являющуюся решением неравенства. Выберем точку, не лежащую на границе, например,
. Определим полуплоскость, являющуюся решением неравенства. Выберем точку, не лежащую на границе, например, 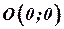 и проверим, удовлетворяет ли она неравенству:
и проверим, удовлетворяет ли она неравенству:  верно. Значит, решением неравенства является полуплоскость, содержащая начало координат. Отметим это штриховкой или стрелкой. Для более компактного решения поступают так: строят границы; определяют полуплоскости.
верно. Значит, решением неравенства является полуплоскость, содержащая начало координат. Отметим это штриховкой или стрелкой. Для более компактного решения поступают так: строят границы; определяют полуплоскости. 

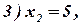
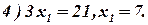
Условие не отрицательности переменных 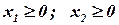 показывает, что область допустимых решений расположена в первой четверти.
показывает, что область допустимых решений расположена в первой четверти. 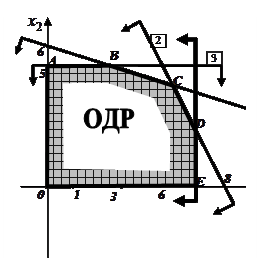
Область допустимых решений – шестиугольник OABCDЕ. Определим координаты вершин (угловых точек):
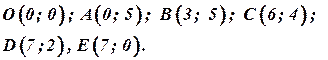
Вычислим значения целевой функции 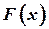 в угловых точках:
в угловых точках: 

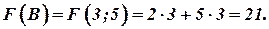
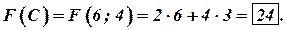
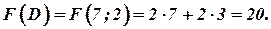

Сравнив значения целевой функции, выберем наибольшее значение: 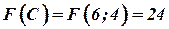 . Итак, если произвести 6 единиц продукции
. Итак, если произвести 6 единиц продукции 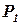 и 4 единицы продукции
и 4 единицы продукции 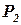 , то получим наибольшую прибыль, равную 24 р.
, то получим наибольшую прибыль, равную 24 р.
Ответ: 
Рассмотренный метод называют перебором всех вершин.
Алгоритм метода «перебора всех вершин»
1. построить область допустимых решений;
2. найти координаты вершин;
3. вычислить значения функции в вершинах;
4. сравнить значения целевой функции;
5. выбрать наименьшее (наибольшее) значение целевой функции, согласно условию задач.
Не нашли, что искали? Воспользуйтесь поиском: