Язык и табличное построение КЛВ.

Логика высказываний (пропозициональная логика) – это теория, изучающая логическую структуру сложных высказываний, отношения между ними и выводы, построенные с учетом этой структуры. При выявлении логических форм контекстов естественного языка в этой теории происходит абстрагирование от содержаний простых высказываний, от их внутренней структуры, а учитывается лишь то, с помощью каких союзов и в каком порядке простые высказывания сочленяются в сложные. Алфавит логики высказываний включает в себя три вида символов:

1) пропозициональные переменные – p, q, r, s,...

2) пропозициональные связки –, &, ∨, ∨, ⊃, ≡

3) скобки – (,).

Пропозициональные переменные замещают собой простые высказывания. Например, высказывание «идет дождь» можно обозначить символом p, высказывание «светит солнце» – символом q, и т.д. Пропозициональные связки предназначены для того, чтобы

объединять простые высказывания в более сложные. Их аналогом в естественном языке чаще всего выступают грамматические союзы.

– отрицание («не»; «неверно, что», «неправда, что» и т.п.)

& – конъюнкция («и», «а», «но», «хотя», и т.п.)

∨ дизъюнкция («или», «по крайней мере одно из двух» и т.п.)

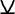– строгая дизъюнкция («либо-либо», «только одно из двух» ит.п.)

⊃– импликация («если, то», «значит», «вытекает» и т.п.)

≡ – эквиваленция («если и только если», «равнозначно» и т.п.)

Значимые выражения в языке КЛВ называются формулами.

Пропозициональные переменные сами по себе уже являются(атомарными) формулами. Более сложные формулы получаются из атомарных с использованием связок. Если А и В – формулы, то А, А&В, А ∨ В, А 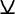В, А ⊃ В, А ≡ В – тоже формулы. Ничто другое не является формулой. Формула, входящая в состав некоторой формулы, называется ее подформулой и выделяется скобками.

Семантика языка КЛВ задается с помощью так называемых «таблиц истинности».

Таблица истинности - это таблица, которая показывает, при каких наборах значений простых высказываний образованное из них сложное высказывание будет истинным, а при каких - ложным.

Алгоритм построения таблицы истинности:

1) Определить число строк (оно вычисляется по формуле k = 2n, где k – количество строк, а n – число различных пропозициональных переменных, входящих в формулу).

2) Задать все комбинации совместной истинности/ложности пропозициональных переменных.

3) Вычислить (построчно) значение каждой подформулы и формулы в целом (используя данное выше табличное определение

пропозициональных связок).

Логика высказываний — это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и отвлекаясь от внутренней структуры суждений.

Под высказыванием принято понимать языковое предложение, о котором имеет смысл говорить, что оно истинно или ложно.

В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний.

Таким образом, законы логики – это такие сложные суждения, которые являются истинными в силу своей логической формы, т.е. только на основании связи составляющих их суждений.

Не нашли, что искали? Воспользуйтесь поиском: