Тема 4. Комбинаторные методы решения логических задач

1. Повторение определений основных понятий темы.

2. Решить задачи.

а) В городе проходит футбольное первенство, в котором участвуют 8 команд. Разыгрываются золотые, серебряные и бронзовые медали (медали получает одна команда). Сколько различных вариантов распределения медалей существует?

б) Сколькими способами можно распределить 5 должностей между 5 лицами, избранными в президиум научного общества?

в) В полуфинале первенства России по шахматам участвуют 10 человек. В финал выходят 3 человека. Определить число различных исходов полуфинала шахматного турнира.

г) Автомобильные номера состоят из трех букв (всего 30 букв) и четырех цифр (используется 10 цифр). Сколько автомобилей можно пронумеровать таким способом, чтобы никакие два автомобили не имели одинаковые номера?

д) Сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?

На дом

а) Группа состоит из 25 человек. Необходимо выбрать старосту, заместителя старосты и профорга. Сколькими способами может быть сделан этот выбор, если каждый член группы может занимать лишь один пост?

б) В магазине имеется 10 ящиков для размещения сумок покупателей. В магазин пришло 10 покупателей. Сколькими способами они могут разместить свои сумки?

в) Сколько существует способов распределения 4 билетов на дискотеку между 20 студентами группы, если каждому студент может получить не больше 1 билета? А сколько существует способов распределения, если 2 билета выделяются девушкам, а 2 – юношам (в группе 8 юношей и 12 девушек)?

г) Сколько различных двухзначных чисел можно образовать из цифр 1,2,3,4.

д) Сколько различных букетов из 9 цветов можно составить, если в продаже имеется 5 видов цветов?

3. Решить задачи, используя бином Ньютона.

а) Найдите наибольший коэффициент разложения (a+b)ⁿ, если сумма всех коэффициентов равна 4096.

б) Найдите член разложения , не содержащий х.

На дом

а) Найдите член разложения , не содержащий х.

б) Коэффициент х во втором члене разложения 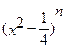равен 31. Найдите степень n.

4. Возвести в шестую степень двучлен, используя треугольник Паскаля для нахождения биномиальных коэффициентов:

(1+ x) на дом (x ²– y).

Не нашли, что искали? Воспользуйтесь поиском: