Площадь поверхности тела вращения

М_i B

А

х

x_i

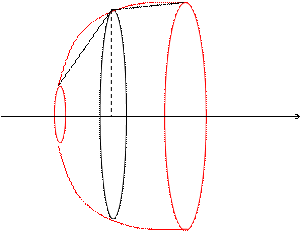
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

Разобьем дугу АВ на n частей точками M₀, M₁, M₂, …, M_n. Координаты вершин полученной ломаной имеют координаты x_i и y_i. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DP_i. Эта площадь может быть найдена по формуле:

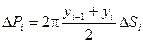
Здесь DS_i – длина каждой хорды.

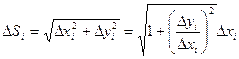
Применяем теорему Лагранжа к отношению .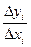

Получаем:

Тогда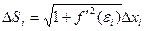

Площадь поверхности, описанной ломаной равна:

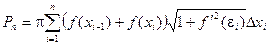
Эта сумма не является интегральной, но можно показать, что

Тогда 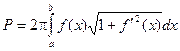- формула вычисления площади поверхности тела вращения.

Кратные интегралы.

Как известно, интегрирование является процессом суммирования. Однако суммирование может производится неоднократно, что приводит нас к понятию кратных интегралов. Рассмотрение этого вопроса начнем с рассмотрения двойных интегралов.

Двойные интегралы

Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой

f(x, y) = 0.

y

0 x

Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область D.

С геометрической точки зрения D - площадь фигуры, ограниченной контуром.

Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dх_i, а по оси у – на Dу_i. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.

Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны S_i = Dx_i × Dy_i.

В каждой частичной области возьмем произвольную точку Р(х_i, y_i) и составим интегральную сумму

где f – функция непрерывная и однозначная для всех точек области D.

Если бесконечно увеличивать количество частичных областей D_i, тогда, очевидно, площадь каждого частичного участка S_i стремится к нулю.

Определение: Если при стремлении к нулю шага разбиения области D интегральные суммы 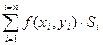имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.

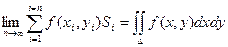
С учетом того, что S_i = Dx_i × Dy_i получаем:

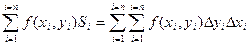
В приведенной выше записи имеются два знака S, т.к. суммирование производится по двум переменным х и у.

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

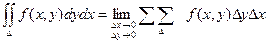
Не нашли, что искали? Воспользуйтесь поиском: