Теоретические основы достоверности

В процессе измерения любой физической величины на получение достоверного результата оказывают влияние многочисленные факторы, включая: особенности органов чувств человека, неоднородности характеристик измеряемых объектов и самих технических средств измерений. Несмотря на то, что в ходе измерений принимаются все меры к сохранению неизменными условий их выполнения, нет гарантии, что получаемые результаты будут одинаковыми. Всегда наблюдается некоторый разброс данных измерений.

В математической статистике и теории вероятностей всякая переменная величина, принимающая различные значения с определенными вероятностями, называется случайной величиной.

Простым и достаточно хорошо всем известным примером такой величины является результат бросания игральной кости (кубика). Число очков, выпадающее на верхней грани игральной кости, представляет собой случайную величину, принимающую значения от 1 до 6 с вероятностью появления каждого, равной ¹/₆.

При выполнении измерений, как правило, встречаются задачи 2-х типов: в первом случае измеряют одну и ту же характеристику у нескольких однородных предметов, во втором случае - несколько раз эту же характеристику у одного предмета. Техническая сущность решаемых задач может быть разная, но в любом случае измеряемая величина носит случайный характер. Это следует из того, что второй случай может быть сведен к первому, если каждое новое измерение будем рассматривать как измерение, выполненное на новом предмете.

Принято (для удобства рассуждений) случайную величину обозначать буквой Х. При выполнении конкретных расчетов букву Х заменяют символом, присвоенным физической величине. Например, при измерении диаметра, то вместо Х пишут d (или D), если измеряют длину, то Х заменяют L (или l) и т. д.

Жизненный опыт показывает, что с увеличением числа измерений уверенность в достоверности полученных результатов возрастает. Рассмотрим зависимость величины доверительной вероятности от количества выполненных измерений (n) на хорошо известном примере – стрельбе по мишени.

Поскольку в математике принято, что вероятностькакого-либо события приблизительно равна частоте f (x) появления его, то она может быть рассчитана по зависимости: , где m – количество появлений наблюдаемого события; п – число проведенных опытов.

Например, если из 100 выстрелов в цель попало 37 пуль, тогда f(x) = = 0,37. Количество опытов п (в приведенном примере – количество выполненных выстрелов), при которых наблюдают событие m (попадание пули в мишень), должно быть достаточно большим. Только в этом случае можно судить о стабильности свойств этого и любого другого изучаемого явления, носящего вероятностный характер.

На основании этого допущения предполагают, что и при выполнении одного единственного выстрела численное значение f (x) = 0,37 сохранится.

Если величину частоты f (x) появления некоторой величины Х обозначить отрезком по оси ординат, то графически это можно представить следующим образом:

Рисунок 1.1 - Распределение частоты f (x) появления отдельных событий Х _i где – центр распределения.

При этом окажется, что ряд результатов совпадут друг с другом или будут очень близкими.

Весь диапазон значений Х (при большом числе наблюдений 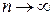) можно разбить на бесконечно малые интервалы dx, и тогда эти данные предстанут в виде некоторой плавной кривой, которую называют плотностью вероятности или нормальным законом распределения (распределение Гаусса) некоторой случайной величины Х:

Рисунок 1.2 - Распределение нормальное случайной величины Х.

Разницу предельных значений называют размахом результатов измерений - .

Разницу отклонений предельных значений от среднего и называют рассеянием случайной величины Х.

Для характеристики распределения случайной величины Х. принимают:

математическое ожидание М (Х) = (центр распределения, он же – среднеарифметическое значение величины);

дисперсию D(Х)=М 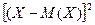, как математическое ожидание квадрата разности между величиной отклонения i-того значения величины от М (Х) = .

Не нашли, что искали? Воспользуйтесь поиском: