
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретические основы точности измерений физических величин
Из определения действительного значения физической величины (приложение №1) следует, чтоэтотакое её значение, которое получено экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него, П огрешностью измерения называют отклонение результата измерения от истинного (действительного) значения измеряемой величины. Таким образом, приведенное ранее определение дисперсии D(Х) характеризует погрешность результата измерения искомой величины.
Для характеристики рассеяния принято использовать основное отклонение, обозначаемое буквой 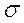 и рассчитываемое по уравнению:
и рассчитываемое по уравнению:
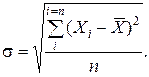
Из него видно: чем больше число измерений n, тем рассеяние меньше, и, следовательно, результат будет более точным. При большом количестве измерений (как правило, более 20 выполненных измерений) такое распределение называют нормальным. Аналитически нормальное распределение описывают зависимостью:
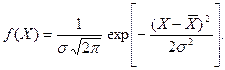
Площадь под нормальной кривой рисунок 3), заключенная внутри промежутка от среднего значения до соответствующего количества единиц основного отклонения (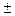
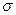 ,
, 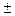 2
2 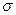 ,
, 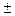 3
3 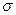 ,
, 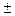 4
4 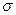 ), численно равна вероятности Р того факта, что действительное значение отклонения от среднего значения будет содержаться внутри указанных интервалов:
), численно равна вероятности Р того факта, что действительное значение отклонения от среднего значения будет содержаться внутри указанных интервалов:

Рисунок 1.3 - Вероятность попадания измерений в заданный доверительный интервал.
Теория вероятностей и накопленный опыт измерений показывают, что максимальные значения разницы 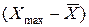 и
и 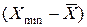 численно не превышают четырех основных отклонений (4
численно не превышают четырех основных отклонений (4 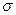 ).
).
Принято такую вероятность (Р) называть доверительной вероятностью, что означает гарантию попадания отдельного результата измерения в заданный интервал.
Из приведенных формул видно, что значения случайной величины 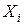 , отклоняющиеся в обе стороны от среднего значения
, отклоняющиеся в обе стороны от среднего значения 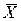 не более чем на величину основного отклонения
не более чем на величину основного отклонения 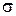 , могут встретиться в 683 случаях на 1000 измерений. Аналогично для 2
, могут встретиться в 683 случаях на 1000 измерений. Аналогично для 2 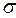 – это составит 954 случая, для 3
– это составит 954 случая, для 3 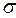 – 997 случаев.
– 997 случаев.
Выполнение большого количества измерений связано со значительными трудозатратами и поэтому неэкономично. В связи с этим интерес представляет получение достаточно достоверных, гарантированных с заданной доверительной вероятностью (Р), и точных результатов при минимуме экспериментального материала за счет уменьшения количества выполняемых измерений.
Эту задачу решают на основе распределения Стьюдента. Сущность его состоит в том, что при переходе от 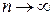 к малым числам n = 2 … 10 доля больших погрешностей возрастает, а доля малых - уменьшается.
к малым числам n = 2 … 10 доля больших погрешностей возрастает, а доля малых - уменьшается.
Последнее обстоятельство хорошо видно из сравнения графического представления распределений Гаусса и Стьюдента (рисунок 4).
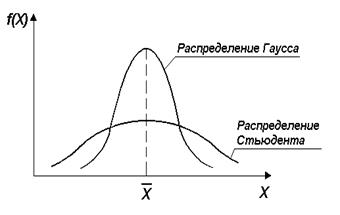
Рисунок 1.4 - Графическая интерпретация распределений Гаусса и Стьюдента.
В силу отмеченных обстоятельств на практике пользуются распределением Стьюдента. Хотя сразу же необходимо заметить, что при 20 -25 измерениях это распределение дает почти такие же результаты, что и нормальное распределение (распределение Гаусса).
В этом случае (как компенсацию меньшего числа проведенных опытов) вместо основного отклонения 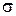 применяют среднюю квадратическую погрешность (
применяют среднюю квадратическую погрешность (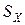 ) результата измерения среднего арифметического значения:
) результата измерения среднего арифметического значения:
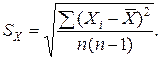
В отличие от нормального распределения, где величина отклонения кратна целому числу 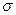 (
(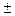
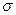 ,
, 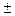 2
2 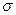 ,
, 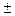 3
3 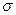 ,
, 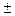 4
4 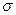 ), в распределении Стьюдента вместо этих чисел применяют коэффициент (статистику) Стьюдента
), в распределении Стьюдента вместо этих чисел применяют коэффициент (статистику) Стьюдента 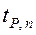 .
.
Нижние индексы у символа коэффициента  означают, что его значение зависит от величины доверительной вероятности результатов измерения (Р) и количества выполняемых опытов (n). Численные значения
означают, что его значение зависит от величины доверительной вероятности результатов измерения (Р) и количества выполняемых опытов (n). Численные значения  принимают из специальных таблиц в зависимости от принятых значений Р и n.
принимают из специальных таблиц в зависимости от принятых значений Р и n.
Как ранее указано, величина доверительной вероятности не может быть менее 0,95 (ибо всякое событие, вероятность которого менее этой величины, считают мало достоверным). С другой стороны, большее ее значение (Р= 0,99; 0,999 и т. д.) должно быть заранее, каким-либо научно-практическим способом, обосновано, исходя из важности социальной или экономической значимости выполняемых измерений. Тогда доверительный интервал ( ), соответствующий принятой величине доверительной вероятности, будет равен:
), соответствующий принятой величине доверительной вероятности, будет равен: 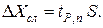 Таким образом, коэффициент Стьюдента
Таким образом, коэффициент Стьюдента  увеличивает величину случайного отклонения, возникающую за счет уменьшения числа измерений. Истинное значение измеряемой величины будет (при принятой заранее величине доверительной вероятности) находиться в интервале:
увеличивает величину случайного отклонения, возникающую за счет уменьшения числа измерений. Истинное значение измеряемой величины будет (при принятой заранее величине доверительной вероятности) находиться в интервале: 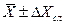 .
.
Итоговая величина погрешности измерения зависит от многих факторов, главными из которых являются метод оценки измерений (прямые или косвенные), средняя квадратическая погрешность средств измерения и границы доверительной погрешности.
Не нашли, что искали? Воспользуйтесь поиском: