Формирование геометрических представлений и изучения методики обучения геометрическим понятиям

Основными задачами изучения геометрического материала в 1-3 классах являются:

1) формирование геометрических представлений;

2) формирование пространственных представлений и развитие воображения, умений наблюдать, сравнивать, абстрагировать и обобщать;

3) выработка у учащихся практических навыков измерения и построения геометрических фигур с помощью измерительных и чертежных инструментов;

4) формирование умений использовать наглядность в приобретении знаний.

Изучение геометрической фигуры осуществляется по такой схеме:

получение фигуры

название фигуры

распознавание фигуры в окружающей обстановке

построение фигуры

изучение свойств

В 1 классе учащиеся уже при поступлении имеют определенные пространственные представления: слева - справа, впереди - позади, вверху - внизу, выше - ниже и т.д. В подготовительный период учитель еще раз предметами, рисунками учебника уточняет эти представления. Выясняет так же знание названий простейших геометрических фигур: треугольника, четырехугольника, круга и др. Эти названия нужны будут при работе с наглядными пособиями (кружками, квадратами и др.) еще до введения понятия об этих фигурах.

Точка и отрезок

В традиционной программе начальной школы изучение геометрического материала начинается с изучения точки и отрезка. В других программам и системах обучения учащиеся знакомятся и с такими понятиями, как линия, прямая, кривая линия, луч, ломаная, звенья ломаной, замкнутые и незамкнутые линии. Ниже, в таблице 29 приводим, как ученику можно дать элементарное представление об этих фигурах.

Таблица 29

Зная вопросы общей методики и схему изучения геометрической фигуры, нетрудно составить текст беседы по изучению определенной фигуры.

С точкой дети знакомятся на первых же уроках, как только берут в руки карандаш.

Понятием отрезка и его длины учащиеся знакомятся во 2 классе. После получения наглядной модели (см.таблицу 29) они показывают, какие предметы в классе имеют вид отрезка (указка, край стола, парты и т.д.). После этого чертят отрезок.

Отмечают две точки, прикладывая к ним линейку, соединяют их линией и получают отрезок. Многие учителя с отрезком знакомят уже в 1 классе в связи с изображением условия задачи с помощью отрезков. Это не приводит к перегрузке, т.к. учащиеся уже имеют практические представления о расстоянии, о сложении расстояния и т.п. В связи с решением задач, некоторые учителя, и обозначение отрезков вводят намного раньше.

Во 2 классе, после изучения понятия отрезка полезно выполнять следующие упражнения:

1) Отметь на бумаге три точки и соедини их попарно отрезками. Сколько отрезков получится?

2) Какую фигуру образуют построенные отрезки?

3) Отметь на отрезке АВ точку С. Сколько отрезков на полученном чертеже? Из каких отрезков состоит отрезок АВ?

В ходе изучения геометрических фигур точка и отрезок приобретают другие свойства: они становятся их вершиной, стороной и др.. При решении задач с взаимопроникающими элементами (см.гл.3, � 3) отрезки становятся общей стороной двух фигур.

Многоугольник, угол, круг

Большинство детей уже в опыте, предшествующем школьному обучению многоугольниками. Они уже знакомы с такой фигурой, как круг. Сравнивая с ним целесообразно ознакомить с понятием многоугольника.

Учитель демонстрирует модели круга, треугольника, четырехугольника и пятиугольника. Выясняют, что у последних имеются углы: три угла, четыре угла, пять углов. Их называют: треугольник, четырехугольник, пятиугольник. Выясняют, что они имеют не только угол, но и стороны, определяют число сторон и углов, показывают на модели.

В 3 классе рассматривают модели треугольника, четырехугольника и т.д. и называют их одним словом многоугольники, т.е. делают обобщение. После введения обозначения точки как "имени", эти фигуры уже называют "именами": отрезок АВ, треугольник АВС, стороны треугольника - АВ, ВС,

АС, вершины - угол А, угол В, угол С.

После ознакомления с многоугольниками учащиеся в окружающей обстановке называют или показывают предметы, имеющие форму соответствующего многоугольника, показывают углы, стороны, вершины. Для стимулирования умственной деятельности учащихся полезно предлагать упражнения такого вида:

1) Какие фигуры изображены на рис.?

1 - кривая линия, 2 - отрезок прямой, 3 - точка, 4 � замкнутая кривая линия, 5 - круг, 6 - замкнутая ломаная линия, 7 - четырехугольник, 8 - пятиугольник, 9 - десятиугольник, 10 - прямая линия, 11 - ломаная линия.

2) Сколько сторон (вершин) у многоугольника 7 (8, 9)? Сколько звеньев у ломаной 6(11)?

Постепенно можно предлагать детям и более сложные задания.

Дети рассказывают (и показывают): "На этом чертеже изображены четырехугольник, два треугольника, пять отрезков".

Первые сведения об углах учащиеся получают в процессе работы с многоугольниками. При получении модели угла учащимся демонстрируем оторванные углы треугольника и выясняем, что угол образуют две стороны и вершина. где соединяются эти стороны. Для ознакомления с прямым углом демонстрируем модели прямоугольника, четырехугольника с тупым и острым углом. Отрываем прямой, тупой и острый углы и сравнением выясняем, что все эти углы разные. После этого сообщаем: "Вот этот угол называется прямым углом (показываю), а эти - непрямые". После этого учащимся рекомендуется самим получить прямой угол с перегибанием листа бумаги неопределенной формы: они дважды перегибают лист бумаги пополам.

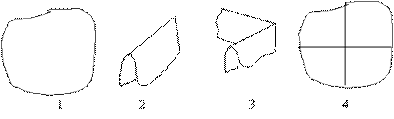
Учащимся показывается чертежный треугольник с прямым углом и наложением прямого угла на разные углы показывается, как определить прямой угол. Предлагается назвать предметы, имеющие прямой угол.

С помощью модели прямого угла учащиеся проверяют, что углы клетки на странице тетради - прямые. Поэтому прямой угол можно нарисовать, используя разлиновку листа тетради. Учащиеся под руководством учителя чертят прямой угол. Для закрепления понятия прямого угла предлагаются упражнения:

1) Найдите прямые углы в предложенных многоугольниках (предлагаются модели, чертежи).

2) Начертите треугольник, имеющий прямой угол.

После усвоения понятия прямого угла, учащиеся знакомятся с прямоугольником как четырехугольником, у которого все углы прямые. С этой целью следует использовать наглядные пособия: вырезать из цветной бумаги и прикрепить на доске несколько четырехугольников, среди которых 2-3 прямоугольника; остальные четырехугольники надо вырезать так, чтобы у одного из них был один прямой угол, у другого - два, у третьего - ни одного.

Детям предлагается установить с помощью угольника, в каких четырехугольниках есть прямые углы. В результате такой работы они увидят, что четырехугольники могут иметь один прямой угол, два прямых угла или же все четыре прямых угла. Учитель сообщает, что четырехугольник, у которого все углы прямые, называется прямоугольником. Аналогичная работа проводится по рисункам учебника.

Для закрепления полученных знаний выполняют упражнения в учебнике. Дети находят прямоугольники, установив предварительно с помощью угольника, что все углы у них прямые. После этого учащиеся называют предметы, имеющие форму прямоугольника и обосновывают свои ответы.

Построение прямоугольника целесообразно предложить после установления свойства прямоугольника: противоположные стороны прямоугольника равны. Это свойство устанавливается, используя его модель и измерением длины сторон. Построение же выполняется, используя разлиновку тетради или же, если есть возможность, использованием чертежного треугольника

с прямым углом.

Методика ознакомления с квадратом аналогична методике ознакомления с прямоугольником. В этом случае из предложенных прямоугольников выделяют тот, у которого все стороны равны. Это и есть квадрат.

В ходе практической работы с моделями и чертежами прямоугольника учащиеся знакомятся с такими понятиями, как противоположные стороны прямоугольника, диагонали прямоугольника и их свойствами: противоположные стороны прямоугольника равны; диагонали прямоугольника (квадрата) равны и в точке пересечения делятся пополам; диагонали квадрата при пересечении образуют прямой угол.

Окружность и круг, как геометрические фигуры, на уроках математики по традиционной программе рассматриваются в 3-м классе. И здесь, используя практическую работу и метод работы с учебником учащиеся усваивают основные термины: окружность � граница круга; центр окружности и круга; радиус и диаметр окружности и круга.

Изучение любого геометрического материала должно быть тесно связано с трудовым обучением.

Задачи с геометрическим содержанием

В начальных классах используются следующие виды задач с геометрическим содержанием:

1. Задачи на составление фигур (см. также гл.3,� 4). Сюда входят такие задания:

а) из счетных палочек постройте треугольник, четырехугольник (1 класс);

б) используя чертеж, начерти два таких треугольника и составь четырехугольник;

в) начерти и вырежь два таких четырехугольник. Составь из них прямоугольник и найди сумму длин его сторон (2 класс);

г) начерти и вырежь такие прямоугольники. Затем сложи из них квадрат (3 класс);

Не нашли, что искали? Воспользуйтесь поиском: