Пояснения к лабораторной работе №3_3. Задание 3

Формулировка задания:

По результатам сдачи сессии группой студентов (таблица Итоги экзаменационной сессии), определить

1. количество сдавших сессию на “отлично” (9 и 10 баллов);

2. на “хорошо” и “отлично” (6-10 баллов);

3. количество неуспевающих (имеющих 3 балла и менее);

4. самый “сложный” предмет;

5. фамилию студента, с наивысшим средним баллом.

Выполнение. Таблица Итоги экзаменационной сессии (ее можно просто скопировать на Лист Задание 3 с Листа Задание 2) имеет слудующий вид:

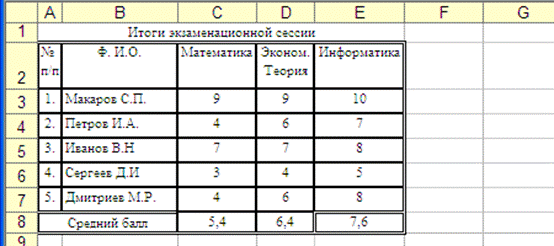
Дополним таблицу двумя столбцами – Средний балл, в которую внесем Средний балл каждого из студентов и Минимальная оценка, в которую внесем минимальную оценку каждого из студентов, полученную во время сессии.

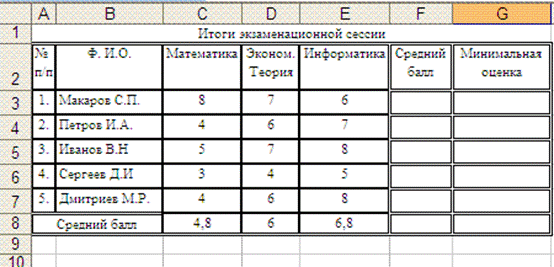
Сначала заполним ячейку Средний балл студента Макарова С.П. (ячейку F3), внеся в нее (например, с помощью кнопки Автосумма, выбрав функцию Среднее ) формулу =СРЗНАЧ(C3:E3), с помощью которой вычисляется среднее из трех чисел (в данном случае – трех оценок).

Затем заполним ячейку Минимальная оценка студента Макарова С.П. (ячейку G3), внеся в нее (например, с помощью мастера функций, вызванного нажатием кнопки fx) формулу =МИН(C3:E3), с помощью которой будет определена минимальная из трех оценок, полученная этим студентом:

Далее выделим ячейки F3 и G3, подведем курсор мыши к правому нижнему углу ячейки G3 так, чтобы он принял вид маркера автозаполнения (“ черный крестик “), и, нажав на левую кнопку мыши скопируем содержимое ячеек F3 и G3 в диапазон F4:G7, где должны размещаться средние и минимальные оценки за сессию всех остальных студентов:

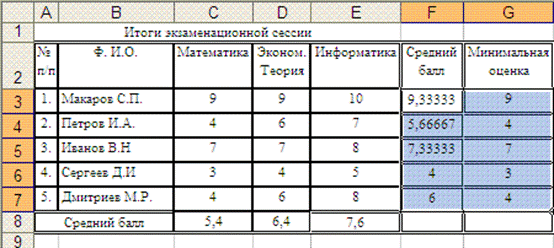
Затем определи количество студентов, (1) сдавших сессию на отлично (9 и 10 баллов), (2) на хорошо и отлично (6-10 баллов) и (3) количество неуспевающих студентов (имеющих 2 балла) и внесем результаты в ячейки E11, E12, E13 соответственно.

1. Очевидно, что у тех, кто сдал сессию на отлично средний балл будет больше либо равен 9. Таким образом, для определения количества отличников с использованием функции СЧЕТЕСЛИ() произведем подсчет количества таких студентов, то есть подсчет количества значений больших либо равных 9 в диапазоне F3:F7, в который внесены средние баллы студентов. Результат выполнения функции =СЧЁТЕСЛИ(F3:F7;">=9") внесем в ячейку E11.

2. Для подсчета количества сдавших сессию на “хорошо” и “отлично” воспользуемся столбцом Минимальная оценка. У таких студенов минимальная оценка будет больше либо равна 6. С использованием функции СЧЕТЕСЛИ() произведем подсчет количества таких студентов, то есть подсчет количества значений больших либо равных 6 в диапазоне G3:G7, в который внесена минимальная оценка, полученная каждым студентом за сессию. Результат выполнения функции =СЧЁТЕСЛИ(G3:G7;">=6") внесем в ячейку E12.

3. Для подсчета количества неуспевающих студентов вновь воспользуемся столбцом Минимальная оценка. У таких студенов минимальная оценка очевидно, будет больше либо равна 3. С использованием функции СЧЕТЕСЛИ() произведем подсчет количества таких студентов, то есть подсчет количества значений меньших либо равных 3 в диапазоне G3:G7, в который внесена минимальная оценка, полученная каждым студентом за сессию. Результат выполнения функции =СЧЁТЕСЛИ(G3:G7;"<=3") внесем в ячейку E13:

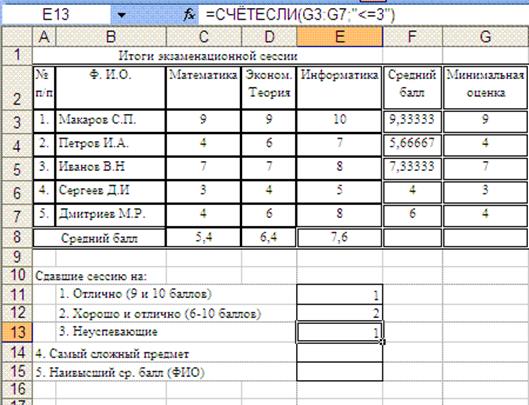
Остается лишь определить (4) самый сложный предмет и (5) ФИОстудента, получившего наивысший средний балл. Очевидно, что самым сложным предметом является тот, по которому средний балл, полученный студентами минимальный из трех возможных вариантов.

Минимальное число из нескольких можно определить с помощью функции Excel МИН(), в данном случае, эту функцию надо применить к диапазону данных C8:E8, в котором ранее подсчитаны средние баллы по предметам (=МИН(C8:E8)).

Остается лишь определить, какому из предметов будет соответствовать минимальная из трех средних оценок. Для этого внесем в ячейку E14 формулу =ЕСЛИ(C8=МИН(C8:E8);C2;ЕСЛИ(D8=МИН(C8:E8);D2;E2)) и при имеющихся исходных данных будет получен результат Математика.

Данная формула содержит две вложенные функции ЕСЛИ().

• Для первой функции в качестве условия (Логического выражения) записано равенство C8=МИН(C8:E8) (в ячейке C8 содержится средний балл по предмету Математика, в случае его выполнения (т.е. минимальный из средних баллов получен по этому предмету) в качестве результата будет выдано содержимое ячейки C2 (то есть название предмета - Математика). В случае же невыполнения условия необходима проверка второго условия (осуществляемая с помощью второй вложенной функции ЕСЛИ().
• Вторая функция ЕСЛИ() осуществляет проверку условия D8=МИН(C8:E8) (в ячейке D8 содержится средний балл по предмету Эконом. Теория, в случае выполнения в результате будет выдано содеожимое ячейки D2 (то есть название предмета – Эконом.теория). В случе невыполнения и этого условия самым сложным предметом будет третий из трех предметов (раз первые два исключены из рассмотрения) - Информатика (его название – в ячейке E2).

Наконец, для определения (5) ФИО студента, получивший наивысший средний балл будут задействованы функции МАКС() (с помощью которой определяется максимальное из группы чисел) и опять же ЕСЛИ(). При определении необходимо последовательно сравнить максимальный из пяти возможных средний балл МАКС(F3:F7) со средним баллом каждого из пяти студентов, и в случае совпадения выдать в качестве резальтата фамилию этого студента.

Соответственно, будут задействованы 4 (на 1 меньше количества студентов) функции ЕСЛИ(), одна – внешняя и три вложенные. Результирующая формула будет иметь следующий вид:

=ЕСЛИ(F3=МАКС(F3:F7);B3;ЕСЛИ(F4=МАКС(F3:F7);B4;ЕСЛИ(F5=МАКС(F3:F7);B5;ЕСЛИ(F6=МАКС(F3:F7);B6;B7))))

В результате внесения данной функции в ячейку E15 будет получено слудующее:

Не нашли, что искали? Воспользуйтесь поиском: