Вопрос 1. Действительные числа.

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

ТЕМА. ВВЕДЕНИЕ В АНАЛИЗ.

Вопрос 1. Действительные числа.

Математический анализ – одно из главных изобретений математики «нового времени». Основополагающие результаты его были получены в 17-18 вв. Декартом, Ньютоном, Лейбницем, Эйлером и другими учеными. Создание математического анализа происходило одновременно с бурным развитием промышленности, естественных наук и в значительной мере было вызвано потребностями в выполнении инженерных расчётов и в теоретическом осмыслении природных процессов.

Предметом изучения анализа являются переменные величины (процессы) и соотношения между ними. При этом основываются на понятии числа, которое назовем действительным числом в отличие от комплексного, потребность в котором возникнет в дальнейшем. Отметим, что любое действительное число можно записать конечной или бесконечной десятичной дробью, например, 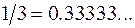, . При введении масштаба измерения любое действительное число можно представить отрезком определенной длины. Благодаря последнему свойству, действительные числа изображают точками на числовой оси. (Числовая ось – направленная прямая с фиксированной точкой отсчета и выбранным масштабом измерения. Положительные числа откладываются от точки отсчета в направлении оси, отрицательные – в противоположном направлении.) Абсолютной величиной числа “ 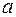” называют неотрицательное число , вводимое по правилу

Абсолютная величина числа указывает расстояние от точки отсчета до точки, изображающей данное число на оси. Для абсолютных величин выполняются неравенства

.

Множество действительных чисел “ ”, удовлетворяющих неравенству , называют закрытым интервалом и обозначают . Если неравенство строгое , то интервал называют открытым и пишут . Комбинации открытого и закрытого интервалов образуют полуоткрытые интервалы

и .

Если хотят показать множество чисел «» для которых выполняется неравенство , то пишут интервал бесконечной длины или при . Символом бесконечности обозначается неограниченная длина интервала.

Не нашли, что искали? Воспользуйтесь поиском: