ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приложения производной. Функции нескольких переменных
71–80. Исследовать функцию методами дифференциального исчисления.
Исследование функции рекомендуется проводить по следующей схеме.
1. Найти область определения функции D(y).
2. Исследовать функцию на четность и нечетность.
3. Найти точки пересечения графика функции с осями координат, если это возможно.
4. Найти интервалы возрастания, убывания и экстремумы функции.
5. Найти интервалы выпуклости и вогнутости, точки перегиба графика функции.
6. По результатам исследования построить график функции.
| № задачи | Функция | № задачи | Функция |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
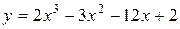
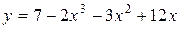
81–90. Дана функция z=f(x, y).
Найти: а) полный дифференциал функции;
б) частные производные второго порядка 
.
| № задачи | Функция |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
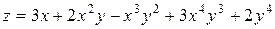
91–100. Дана функция 
и точка 
.
Найти градиент функции в точке А.
| № Задачи | Функция | Координаты точки А | № задачи | Функция | Координаты точки А |
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
|
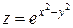
101–110. Экспериментально получены пять значений функции y=f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию вида 
, выражающую приближенно (аппроксимирующую) функцию y=f(x). Сделать чертеж, на котором в декартовой системе координат построить экспериментальные точки и график функции .
| № задачи | Линейная зависимость | № задачи | Линейная зависимость | ||||||||||
| xi | xi | ||||||||||||
| yi | 1,9 | 2,8 | 3,4 | 4,3 | 5,1 | yi | 5,0 | 5,8 | 4,5 | 2,3 | 3,0 | ||
| xi | xi | ||||||||||||
| yi | 5,8 | 7,0 | 5,3 | 3,4 | 3,9 | yi | 4,5 | 5,5 | 4,0 | 2,0 | 2,5 | ||
| xi | xi | ||||||||||||
| yi | 5,8 | 6,7 | 5,3 | 3,2 | 3,7 | yi | 3,5 | 2,7 | 2,0 | 1,3 | 0,5 | ||
| xi | xi | ||||||||||||
| yi | 5,0 | 6,2 | 4,6 | 2,6 | 3,1 | yi | 1,0 | 1,7 | 2,6 | 3,2 | 4,1 | ||
| xi | xi | ||||||||||||
| yi | 5,4 | 6,6 | 5,0 | 3,1 | 3,4 | yi | 3,0 | 3,9 | 4,6 | 5,4 | 6,0 |
Не нашли, что искали? Воспользуйтесь поиском: