Пряма на площині. Різновиди рівнянь прямої.

ЗАДАЧІ ДЛЯ РОЗВ’ЯЗУВАННЯ В АУДИТОРІЇ.

Приклад 7.1. На осі Ox знайти точку, рівновіддалену від початку координат і точки A(-18; -6).

Приклад 7.2. Яку ординату має точка C, що лежить на одній прямій з точками A(3; -1) і B(5; 1) та має абсцису x =8.

Приклад 7.3. Трикутник заданий вершинами А(8; -2), В(0; 6), С(4;-1). Знайти:

а) точки, які поділяють сторону АС на три рівні частини;

б)рівняння сторони АВ;

в)рівняння висоти, проведеної з вершини В.

Приклад 7.4. Трикутник заданий вершинами А(0; -2), В(4; 6), С(-4; 8). Знайти:

а) внутрішній кут В;

б) рівняння медіани, що проходить через вершину В;

в) рівняння прямої, що проходить через вершину С паралельно стороні АВ.

Приклад 7.5. Дано вершини трикутника A(4; 1), B(-3; 3), C(2; -3). Знайти рівняння середньої лінії трикутника, що паралельна стороні AB.

ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РОЗВ’ЯЗУВАННЯ.

Приклад 7.6 При якому значенні 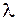точки A(-1;-2), B(2;4), C(3; 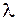) лежать на одній прямій?

Приклад 7.7. Дано вершини чотирикутника A(-1;4), B(4;4), C(5;1), D(-1; 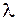). При якому значенні 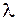його діагоналі перпендикулярні?

Приклад 7.8. Трикутник заданий вершинами А(7; -3), В(0; 4), С(3;-5). Знайти:

а) точки, які поділяють сторону ВС на три рівні частини;

б)рівняння сторони АС;

в)рівняння висоти, проведеної з вершини А.

Приклад 7.9. Трикутник заданий вершинами А(0; -2), В(4; 6), С(-4; 8). Знайти:

а) внутрішній кут А;

б) довжину висоти, що проходить через вершину В;

в) рівняння середньої лінії трикутника, яка паралельна стороні АВ.

Приклад 7.10. Скласти рівняння серединного перпендикуляра до відрізка AB: A(-3; 1), B(5; 3).

Не нашли, что искали? Воспользуйтесь поиском: