
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ II РОДА
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ I РОДА
Определение
Пусть на непрерывной кривой 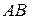 в плоскости
в плоскости  задана функция двух переменных
задана функция двух переменных  .
.
1. Разобьём 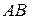 на
на  «элементарных дуг» с длинами
«элементарных дуг» с длинами  .
.
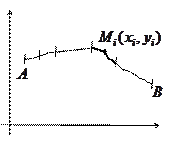 2. Выберем на каждой
2. Выберем на каждой  -той дуге произвольно точку
-той дуге произвольно точку  и вычислим значение функции
и вычислим значение функции  в ней.
в ней.
3. Составим интегральную сумму  .
.
4. Перейдем к пределу при 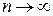 так, чтобы
так, чтобы  . Если существует конечный предел интегральных сумм
. Если существует конечный предел интегральных сумм  и он не зависит ни от способа разбиения на элементарные области, ни от выбор точек в них, его называют криволинейным интегралом I рода от функции
и он не зависит ни от способа разбиения на элементарные области, ни от выбор точек в них, его называют криволинейным интегралом I рода от функции  по кривой
по кривой 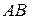 и обозначают
и обозначают
 .
.
Достаточным условием существования криволинейного интеграла I рода является гладкость кривой 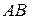 и непрерывность функции
и непрерывность функции  на ней.
на ней.
Основные свойства

 ,
,  – называется средним значением функции
– называется средним значением функции  на кривой
на кривой 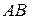 .
.
Правила вычисления
Вычисление криволинейного интеграла I рода сводится к вычислению определенного интеграла.
1. Если кривая задана явно,  , то
, то
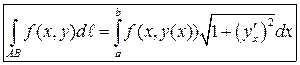 .
.
2. Если кривая задана параметрически, 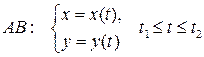 , то
, то
 .
.
3. Если кривая задана в ПСК,  , то
, то
 .
.
 Вычислить интеграл
Вычислить интеграл  , где
, где  .
.
Решение.
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ II РОДА
Определение
Пусть на непрерывной кривой 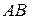 в плоскости
в плоскости  задана вектор-функция двух переменных
задана вектор-функция двух переменных  .
.
1. Точками  разобьём
разобьём 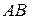 на
на  «элементарных дуг». Каждой
«элементарных дуг». Каждой  -той дуге поставим в соответствие вектор
-той дуге поставим в соответствие вектор  . Его координаты
. Его координаты  обозначим
обозначим  и
и  .
.
2. Выберем на каждой  -той дуге произвольно точку
-той дуге произвольно точку 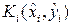 и вычислим значение функции
и вычислим значение функции  в ней.
в ней.
3. Составим интегральную сумму из скалярных произведений
 .
.
 4. Перейдем к пределу при
4. Перейдем к пределу при 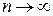 так, чтобы
так, чтобы 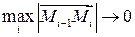 . Если существует конечный предел интегральных сумм и он не зависит ни от способа разбиения на элементарные области, ни от выбор точек в них, его называют криволинейным интегралом II рода от функции
. Если существует конечный предел интегральных сумм и он не зависит ни от способа разбиения на элементарные области, ни от выбор точек в них, его называют криволинейным интегралом II рода от функции  по кривой
по кривой 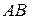 и обозначают
и обозначают
 .
.
Достаточным условием существования криволинейного интеграла II рода является гладкость кривой 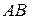 и непрерывность функций
и непрерывность функций  и
и  на ней.
на ней.
Основные свойства

Правила вычисления
Вычисление криволинейного интеграла II рода сводится к вычислению определенного интеграла.
1. Если кривая задана явно,  , то
, то
 .
.
2. Если кривая задана параметрически, 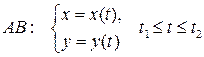 , то
, то
 .
.
 Вычислить интеграл
Вычислить интеграл  , где
, где  .
.
Решение.
Не нашли, что искали? Воспользуйтесь поиском: