Бесконечно малые и бесконечно большие функции.

Иx свойства.

Определение: Функция a(x) называется бесконечно малой при x®x₀, если .

Обозначается a(x) – б/м при x®x₀.

Функция a(x) – б/м при x®x₀, если " >0 $d>0: из |x-x₀| <d Þ |a(х)|< .

Определение: Функция y=f(x) называется ограниченной, если существует такое число M >0, что |f(x)| М при " .

Определение: Функция f(x) называется бесконечно большой при x®x₀, если .

Обозначается f(x) — б/б при x®x₀.

Функция f(x) — б/б при x®x₀, если для любого А>0 найдется d>0: из неравенства |x-x₀|<d следует неравенство |f(x)|>А.

В качестве x₀ может быть конечное число, ±¥ или ¥.

Свойства.

1. Сумма двух или конечного числа б/м есть бесконечно малая.

2. Произведение двух или конечного числа б/м есть бесконечно малая.

3. Произведение б/м на ограниченную функцию есть б/м.

Замечание: Частное двух б/м является неопределенностью вида .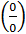

4. Сумма конечного числа б/б есть б/б.

5. Произведение конечного числа б/б есть б/б.

6. Произведение б/б на любую не б/м есть б/б.

Замечание: Разность двух б/б является неопределенностью вида (¥-¥).

Замечание: Частное двух б/б является неопределенностью вида .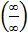

Замечание: Произведение б/б на б/м является неопределенностью вида .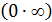

7. Частное от деления б/б на ограниченную функцию есть б/б.

8. Б/м и б/б ‒ взаимообратные функции.

Док-во:

1) б/м есть обратная величина для б/б. .

Пусть f(x) – б/б при x®x₀. Тогда по определению б/б: для любого A>0 такое, что из неравенства |x-x₀| <d будет следовать неравенство |f(x)| >A. Перейдем к обратным величинам: |1/f(x)| < 1/A Þ б/м по определению.

2) б/б есть обратная величина для б/м.

Пусть a(x) – б/м при x®x₀. Тогда по определению: " >0 $ d>0 такое, что из неравенства |x-x₀|<d Þ неравенство |a(x)|< . Перейдем к обратным величинам: |1/a(x)| > 1/ , что означает по определению, что 1/a(x) – б/б величина.

Ч.т.д.

Не нашли, что искали? Воспользуйтесь поиском: