Некоторые определения из теории множеств

Множество – фундаментальное неопределяемое понятие. Множество – это совокупность объектов, которые, с одной стороны, различны и отличимы друг от друга, а с другой стороны воспринимаются как единое целое.

Пусть А и В – два множества.

<a,b> - упорядоченная пара, где первый элемент , а второй элемент .

Декартово произведение - это множество пар

Бинарным отношением f из множества А в множество В называется подмножество :

.

Функция - это такое отношение, что из и следует, что x=z, т. е. функциональность – это однозначность.

Пример.

А={1,2,3,4,5}

B={1,4,9,16,25}

={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, ….,<4,16>,…..<5,25>}

f={<1,1>, <2,4>, <3,9>, <4,16>, <5,25>} – это функция, где b=a².

Булевы функции

Функция 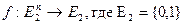называется функцией алгебры логики.

y=f(x₁,x₂) – бинарная функция,

y=f(x₁,x₂,…., x_n) – n- арная функция.

Пример.

Т. о. каждое элементарное высказывание может принимать значение либо 0, либо 1. Каждому набору значений a, b, c соответствует одно значение всего сложного высказывания (0 или 1).

Булеву функцию от n переменных можно задать таблицей истинности

Переменные, которые принимают значения 0 или 1 называются булевыми переменными.

Некоторые функции всегда принимают значение 1 (на любом наборе переменных). Такие функции называются тавтологиями. Некоторые функции всегда принимают значение 0 (на любом наборе переменных). Такие функции называются противоречиями.

Формулы

Пусть - множество булевых функций. Формулой над F называется выражение либо переменная, либо формула над F.

F называется базисом формулы, f – главной (внешней) операцией, t_i – подформулами.

Всякой формуле 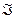однозначно соответствует некоторая функция f. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение функции при заданных значениях переменных.

Зная таблицы истинности для функций базиса можно вычислить таблицу той функции, которую реализует данная формула.

Примеры.

1.

x1	x2	x1 x2

Функция реализует дизъюнкцию на базисе .

2.

x1	x2	x1~ x2

Функция реализует дизъюнкцию на базисе .

Таким образом каждая формула определяет некоторую логическую функцию, которую можно представить в виде таблицы истинности для этой формулы. Если в формуле имеется n переменных, то возможны 2ⁿ различных истинностных значений для этой формулы. Следовательно, таблица истинности будет иметь 2ⁿ строк.

Не нашли, что искали? Воспользуйтесь поиском: