
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Полные системы функций
1.9.1. Система функций {  }
}
Теорема. Всякая булева функция порождается некоторой формулой, в которой есть только операции  .
.
Доказательство. Пусть  некоторая булева функция. Для нее можно поострить таблицу истинности, в которой будет 2n строк. Каждую строку можно представить в виде конъюнкции переменных х1,…хn, куда входит либо
некоторая булева функция. Для нее можно поострить таблицу истинности, в которой будет 2n строк. Каждую строку можно представить в виде конъюнкции переменных х1,…хn, куда входит либо  , либо
, либо  . Если значение конъюнкции будет равно 1, то всю функцию можно представить в виде дизъюнкции этих конъюнкций.
. Если значение конъюнкции будет равно 1, то всю функцию можно представить в виде дизъюнкции этих конъюнкций.
Пример.
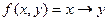
| x | y | f(x,y) |
Получим СДНФ, используя таблицу истинности.
 Возникает вопрос: Существуют ли другие системы булевых функций, с помощью которых можно выразить все другие функции?
Возникает вопрос: Существуют ли другие системы булевых функций, с помощью которых можно выразить все другие функции?
Замкнутые классы
Пусть  множество булевых функций от n переменных.
множество булевых функций от n переменных.
Замыканием F ([F]) называется множество всех булевых функций, реализуемых формулами над F.
Множество функций (класс) называется замкнутым, если [F]=F.
Рассмотрим следующие классы функций.
1. Класс функций, сохраняющих 0:
 .
.
2. Класс функций, сохраняющих 1:
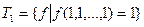
3. Класс самодвойственных функций:
 , где
, где  .
.
4. Класс монотонных функций
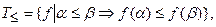 где
где  .
.
5. Класс линейных функций
 , где + - означает сложение по модулю 2, а знак конъюнкции опущен.
, где + - означает сложение по модулю 2, а знак конъюнкции опущен.
Теорема. Классы Т0, Т1, Т*, ТМ, TL – замкнуты.
Доказательство. Чтобы доказать, что некоторый класс F замкнут достаточно показать, что, если формула реализована в виде формулы над F, то она принадлежит F.
Рассмотрим доказательство для одного класса функций Т0.
Пусть  и
и  . Тогда
. Тогда  .
.
Аналогичные доказательства можно привести для остальных классов.
Не нашли, что искали? Воспользуйтесь поиском: