Интерпретация формальных теорий

Интерпретацией формальной теории 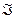в область интерпретации М называется функция , которая каждой формуле формальной теории ставит в соответствие некоторое содержательное высказывание относительно объектов множества М. Если соответствующее высказывание истинно, то говорят, что формула выполняется в интерпретации I.

Интерпретация называется моделью множества формул Г, если все формулы выполняются в данной интерпретации.

Если формула истинна в любой интерпретации, то это тавтология, если формула ложна в любой интерпретации, то это противоречие.

Формальная теория 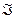называется семантически непротиворечивой, если ни одна ее теорема не является противоречием.

Модель для формальной теории 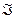существует тогда и только тогда, когда она семантически непротиворечива.

Формальная теория 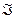формально непротиворечива, если в ней нельзя одновременно вывести формулу F и ее отрицание.

Формальная теория 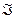называется полной, если каждому истинному высказыванию модели М соответствует теорема теории .

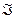Если для множества М существует формально полная непротиворечивая теория 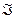, то множество М называется аксиоматизируемым или формализуемым.

Формальная теория 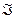называется разрешимой, если существует алгоритм, который определяет, является ли формула теоремой теории.

Не нашли, что искали? Воспользуйтесь поиском: