Исчисление предикатов

Исчисление предикатов первого порядка – это формальная теория K, в которой определены:

1. Алфавит:

· Связки: (основные), &, 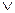(дополнительные).

· Служебные символы: (,).

· Кванторы , .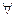

· Предметные константы a,b,c,….

· Предметные переменные x, y, z,….

· Символы предикатов P,Q,R,….

· Символы функций f, g, h,….

Константы, переменные, функторы – называются термами.

2. Формулы. Слово называется формулой, если оно имеет следующий синтаксис:

1) Р(х₁,…,х_n) – атомарная формула (А).

Вхождения переменных в атомарную формулу называются свободными.

2) Если А – формула, то 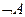- тоже формула.

3) Если А и В – формулы, то - формулы.

4) Если А – формула, содержащая свободную переменную х, то 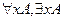- формулы.

Слово является формулой, если это следует из 1-4.

Вхождения переменных в формулах 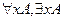называются связанными, переменные не равные х остаются свободными.

Пример

- х – свободная переменная, у – связанная переменная.

Формула, не содержащая свободных переменных, называется замкнутой.

3. Аксиомы (логические).

1) Любая система аксиом исчисления высказываний.

А1:

А2: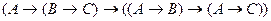

А3:

2) Собственные аксиомы.

P1: ,

P2: ,

где t – терм.

4. Правила вывода.

1. ,

2. - введение квантора общности,

3. 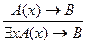- введение квантора существования.

Исчисление предикатов, в котором кванторы могут связывать только предметные переменные и не могут связывать функторы или предикаты называется исчислением первого порядка.

Интерпретация

Интерпретация I исчисления предикатов K с областью интерпретацией M – это набор функций, который сопоставляет:

· каждой предметной константе a элемент I(a)ÎM;

· каждому n-местному функтору f операцию I(f):Mⁿ®M.

· каждому n-местному предикату Р отношение I(P)Ì Mⁿ.

Для нас имеют смысл только интерпретированные предикаты, т. е. те, которым поставлены в соответствие некоторые отношения (для одноместных предикатов – свойства).

Пример.

Рассмотрим 3 формулы.

1. P(x,y)

2.

3.

В качестве области интерпретации возьмем множество целых положительных чисел и интерпретируем P(x,y) как отношение .

Тогда формула 1 – это предикат . Он принимает значение истинно при любых a,b принадлежащих множеству целых положительных чисел, если .

Формула 2 – это предикат, который принимает значение истинно при x=1, т. е. он выражает свойство, что для каждого положительного целого числа y .

Формула 3 – это предикат, который всегда будет истинен. Он выражает свойство: существует положительное целое число y, для которого .

Формула называется истинной, если она выполняется на любом наборе элементов М.

Формула называется ложной, если она не выполняется на любом наборе элементов М.

Формула общезначима (тавтология), если она истинна в любой интерпретации.

Теорема: Любая выводимая в исчислении предикатов формула – общезначима.

Не нашли, что искали? Воспользуйтесь поиском: