Производные правила вывода

Исчисление высказываний £ достаточно богатая формальная теория, в которой можно вывести многие правила вывода.

Теорема 1.

- закон тождества.

Доказательство.

1. А1: . Выполним замену { }. Получим:

.

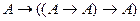2. А1: . Выполним замену { }. Получим:

.

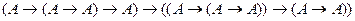3. Из 1 и 2 по правилу m.p. получим:

.

4. A1: {A/B}. Получим: .

5. Из 3 и 4 по правилу m.p. получим .

Теорема 2

А - добавление антцедента.

Доказательство.

1. А - гипотеза

2. А1:

3. Из 1 и 3 по правилу m.p. получаем

Всякую доказанную выводимость можно использовать как новое производное правило вывода.

Если имеется множество общезначимых формул, то из него можно вывести только общезначимые формулы.

Дедукция

В теории £ импликация тесно связана с выводимостью. Теорема дедукции используется при доказательстве теорем, т. к. дает нам новое правило вывода.

Теорема (дедукции). Если Г – множество формул, А и B Î Г и A|-_£B, то Г|-А→В.

В частности A|-B, то А→В.

Доказательство. Пусть E₁,E₂,….E_n вывод B из Г, A. E_n = B. Покажем, что Г|-_£А→ E_i, .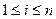

Пусть i=1.

Возможны 3 случая.

1) Пусть Е₁ – аксиома. Тогда рассмотрим вывод:

1. Е₁

2. А1: . Выполним замену {А/Е1, В/А}. Получим:

3. Из 1 и 2 по правилу m.p. получаем |-_£А→ E₁.

2) Пусть Е₁ Г. Доказательство аналогично 1).

3) Пусть Е₁ А. Тогда по закону тождества (теорема1) , следовательно,

Таким образом Г .

Пусть i<k. Рассмотрим вывод E_k. Возможны 4 случая:

1) E_k – аксиома.

2) Е₁ Г.

3) Е₁ А.

4) E_k получена из формул E_i и E_j по правилу m.p., причем i,j<k и E_i=E_j® E_k.

Для 1), 2), 3) доказательство аналогично доказательству при i=1.

Для 4) случая:

1. (i)

2. (j)

3. А2: 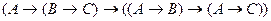. Выполним подстановку {E_i/B, E_k/C}, получим (n)

4. По правилу m.p. из (j) и (n) получаем (n+1)

5. По правилу m.p. из (j) и (n+1) получаем (n+2) ч.т.д.

Таким образом, 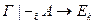для любого k, в том числе при k=n. Но E_n=B Þ .

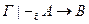Схема аксиом A3 теории £ в доказательстве не использовалась, поэтому теорема дедукции имеет место для более широкого класса теорий, чем £.

Следствие 1. Если 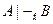, то 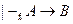и обратно.

Доказательство. По теореме дедукции, если , то 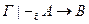. Пусть Г={0}. Тогда имеем Следствие 1.

Следствие 2. (правило транзитивности).

Доказательство.

1. Гипотеза .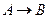

2. Гипотеза с.

3. Гипотеза А.

4. По правилу m.p. из 1 и 3 получаем B.

5. По правилу m.p. из 2 и 4 получаем C

6. Из 1-5 получаем: если 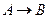, - гипотезы Г, то .

7. По теореме дедукции .

Следствие 3. 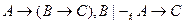(правило сечения).

Доказательство.

1. Гипотеза .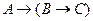

2. Гипотеза A.

3. По правилу m.p. из 1 и 2 получим .

4. В – гипотеза.

5. По правилу m.p. из 3 и 4 получим С.

6. Из 1-5 получаем: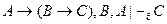

7. по теореме дедукции .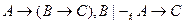

2.9. Некоторые теоремы теории £

Множество теорем теории £ бесконечно. Рассмотрим некоторые из них.

1. (закон двойного отрицания).

2. (закон двойного отрицания).

3. 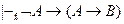(из ложного что угодно).

4. (закон де Моргана)

5. 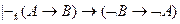(закон де Моргана)

и т. д.

(Вывод законов см. Ф.А. Новиков “Дискретная математика для программистов”, стр.114).

Теорема. Теоремами теории £ являются только общезначимые формулы.

Следствие. Теория £ формально непротиворечива.

Выводы.

1. Можно задать некоторые правила преобразования формул, которые обладают свойством: при применении к общезначимым формулам они дают в результате общезначимые формулы. Такими правилами являются правила вывода.

2. Можно задать конечное число общезначимых формул таких, что любая общезначимая формула может быть получена из них с помощью правил вывода.

Не нашли, что искали? Воспользуйтесь поиском: