Основные равносильности для предикатов

Пусть формулы А и В имеют одно и то же множество свободных переменных (в том числе и пустое).

Формулы А и В равносильны в данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковое значение (т. е. формулы выражают один и тот же предикат).

Формулы А и В равносильны на множестве М, если они равносильны во всех интерпретациях, заданных на множестве М.

Формулы А и В равносильны (),если они равносильны на всех множествах.

· Для формул логики предикатов сохраняются все равносильности логики высказываний.

· Перенос квантора через отрицание

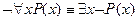
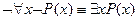
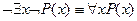
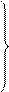· Вынос квантора за скобки

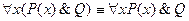
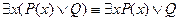
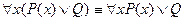
	Q – не зависит от х
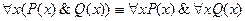
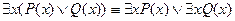
	Q – зависит от х
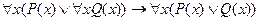
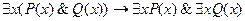
	только в одну сторону!

Пусть P(x) – x пошел в театр, Q(x) – x пошел в кино, тогда

.

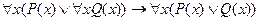Но .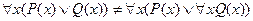

Аналогично, пусть P(x) – x делится на 2, Q(x) – x делится на 3, тогда

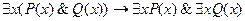, но

.

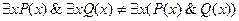· Перестановка одноименных кванторов

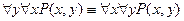
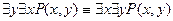
1. Перестановка разноименных кванторов

· Переименование связанных переменных

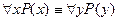
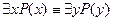
х, у принадлежат одной предметной области

· Отбрасывание квантора

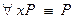
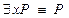
Пример. Докажем общезначимость формулы . Для этого надо показать, что формула является теоремой исчисления предикатов.

Доказательство.

1. 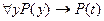- аксиома исчисления предикатов.

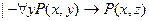
2. 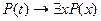- аксиома исчисления предикатов.

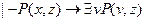
3. Для исчисления высказываний доказано правило транзитивности:

4. Из 1 и 2 по правилу транзитивности получаем:

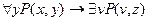
5. Введение квантора существования (правило вывода исчисления предикатов ):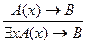

6. Введение квантора общности (правило вывода исчисления предикатов

):

7. Преобразуем связанную переменную {y/z}

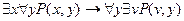
8. Преобразуем связанную переменную {x/v}

Таким образом, теорема доказана.

Не нашли, что искали? Воспользуйтесь поиском: