Тема 3. Логика и исчисление предикатов

Логика высказываний – очень узкая логическая теория. Есть такие типы логических рассуждений, которые не могут быть осуществлены в рамках логики высказываний. Например:

1. Всякий друг Ивана есть друг Петра. Павел не друг Ивана, следовательно, Павел не друг Петра.

2. Простое число 2 – четное, следовательно, существуют четные простые числа.

Корректность таких выводов базируется не только на истинности соответствующих предложений, но и на смысле слов «всякий» и «существуют». Чтобы сделать более понятной структуру сложных высказываний используют специальный язык – язык предикатов первого порядка.

Предикаты

Рассмотрим предложения, зависящие от параметров:

Х – четное число.

X<Y

X+Y=Z

X,Y – братья.

Если заменить переменные X, Y, Z некоторыми конкретными значениями, то мы получим определенные высказывания, которые могут быть истинными или ложными.

Например:

3 – четное число.

2<5

2+3=5

Иван и Павел – братья.

Предложения такого рода называются предикатами.

Предикат Р(х₁,…,х_n) – функция, переменные которой принимают значения из некоторого множества M, а сама функция принимает значение истина (1) или ложь (0).

Р(х₁,…,х_n): M_n®{0,1}

Высказывания - это 0-местные предикаты. Над предикатами выполняются логические операции, в результате чего получаются новые предикаты.

С каждым предикатом связано число, которое называется местностью или арностью предиката (количество переменных).

Язык предикатов – наиболее приближенный к естественным языкам формальный математический язык.

Примеры:

1. Р(х) – х делится на 2

Q(x) – x делится на 3

P(x)&Q(x) – x делится на 2 и 3, т. е. определен предикат делимости на 6.

2. S(x,y) – x равно y.

S(x,y)& S(y,z)®S(x,z)

Кроме операций логики высказываний, к предикатам можно применять операции связывания кванторами.

1. Квантор общности ().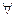

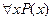- высказывание истинное для каждого , т. е. это высказывание не зависит от x_i.

2. Квантор существования ().

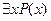- высказывание истинно, если существует , для которого это высказывание истинно.

Для конечных множеств операции навешивания кванторов можно выразить через операции & и .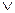

Пусть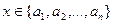

На языке предикатов можно составить более сложные высказывания, чем на языке логики высказываний.

Не нашли, что искали? Воспользуйтесь поиском: