Определение и алгебраическая форма комплексных чисел

Комплексными числами называются выражения вида , (где а и b действительные числа, а - символ, удовлетво­ряющий условию ), при условии, что для этих выражений равенство, сложение и умножение определя­ются следующим образом:

а) два комплексных числа и считаются равными тогда и только тогда, когда и

б) суммой двух комплексных чисел и назы­вается комплексное число (1.1),

в) произведением двух комплексных чисел и на­зывается комплексное число (1.2).

Пример. 1.1. Вычислить сумму и произведение двух комплексных чисел:

Решение.

Из приведенных примеров видно, что формулы (1.1) и (1.2.) помнить необязательно. Сложение и умножение комплексных чисел можно выполнять по правилам сложения и умножения двучленов.

Разность двух комплексных чисел – операция обратная сложению и может быть выполнена по формуле: (1.3).

Пример 1.2. Вычислить разность двух комплексных чисел:

Решение

Из приведенного примера видно, что формулу (1.3) помнить необязательно. Вычитание комплексных чисел можно выполнять по правилам вычитания двучленов

Число называется комплексно-сопряженным с комп­лексным числом . Понятие комплексной сопряженности взаимно.

Сумма и произведение комплексно-сопряженных чисел со­ответственно равны и .

Частное от деления одного комплексного числа на второе – операция обратная умножению и может быть выполнена по формуле:

(1.4)

Эту формулу можно не запоминать, а руководствоваться следующим правилом: для того, чтобы разделить одно комплексное число на другое, надо записать их в виде дроби, в числителе которой – делимое, а в знаменателе – делитель, а затем числитель и знаменатель умножить на число, сопряженное со знаменателем.

Покажем справедливость этого правила:

Как можно увидеть, получившееся в результате использования приведенного выше правила деления комплексных чисел совпадает с правой частью формулы (1.4), что свидетельствует о справедливости этого правила.

Пример 1.3.

Вычислить частное от деления комплексного числа на комплексное число

Решение

В этом примере использованы по сути те же данные, что и во втором из примеров 1.1. В данном случае делимое – результат перемножения комплексных чисел примера 1.1. Делитель – второй из сомножителей упомянутого примера. Частное от деления в текущем примере совпало с первым сомножителем примера 1.1., что подтверждает правильность выполненной нами операции деления.

Комплексное число равно нулю тогда и только тогда, ког­да .

Для комплексных чисел, так же, как и для векторов, нет по­нятия больше и меньше.

Покажем, как в множестве комплексных чисел решаются квадратные уравнения, дискриминанты которых меньше нуля.

Пусть, например, нужно решить уравнение . Легко подсчитать, что

Сле­довательно,

.

Поэтому

То есть, квадратное уравнение с действительными ко­эффициентами и отрицательным дискриминантом имеет два комплексно-сопряженных корня.

Операция возведения в степень комплексного числа рассмат­ривается как частный случай произведения одного и того же со­множителя.

Степени мнимой единицы даются формулой

Например,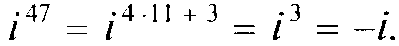

Пример 1.4. Найти действительные числа х и y из уравнения

Решение. Используем условия равенства двух комплексных чисел и .

Пользуясь определени­ем суммы, получаем Сравнивая действите­льные и мнимые части чисел z₁ и z₂, получим систему двух урав­нений относительно х и у , решением которой будет .

Не нашли, что искали? Воспользуйтесь поиском: