ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приложения определенного интеграла в механике
Путь, пройденный телом при неравномерном движении за время 
, вычисляется по формуле:
. (3.18)
Пример 3.18. Скорость движения материальной точки задана уравнением 
. Определить ее путь за четвертую секунду.
Решение. 
.
Ответ 83 м.
Пример 3.19. Скорость движения тела задана уравнением 
м/с. Определить путь, пройденный телом от начала движения до остановки.
Решение Скорость движения тела равна пулю в моменты начала его движения и остановки. Найдем момент остановки тела, для чего приравняем скорость нулю и решим уравнение относительно t:
- пределы интегрирования.
Ответ. S = 32 m.
Работа А, произведенная переменной силой 
при перемещении тела oт 
до 
, вычисляется по формуле:
(3.19),
где 
- в ньютонах (Н); 
- в метрах (м); 
- в джоулях (Дж).
Пример 3.20. Сила в 8Н. растягивает пружину на 6см. Какую работу она производит?
Решение.
Согласно закону Гука 
, где 
- величина растяжения, 
- коэффициент пропорциональности.
Дж.
Ответ: 
Дж.
Формула вычисления силы 
давления жидкости на пластинку, погруженную в жидкость:
, (3.20)
где а - глубина, на которой находится самая верхняя точка пластинки; b - глубина, на которой находится самая нижняя ее точка; х - расстояние точек пластинки до уровня жидкости; 
- плотность жидкости, 
, 
- функция, зависящая от формы пластинки;
Пример 3.21. Треугольная пластинка с основанием 0,2 м и высотой 0,4 м погружена вертикально в воду так, что вершина ее лежит на поверхности воды, а основание параллельно ей (см. рис.). Вычислить силу давления воды па пластинку.
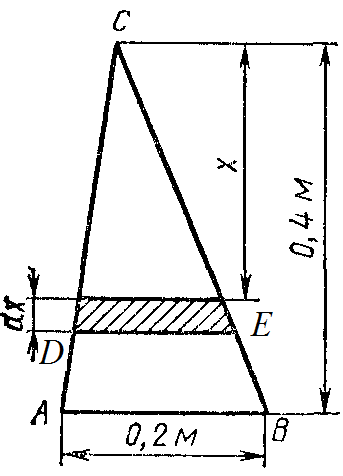Решение. На глубине х выделим горизонтальную полоску шириной dx. Вычислим площадь полоски 
. Из подобия треугольника ABC и DEC имеем:
, откуда 
.
Тогда 
Ответ: 
Приложение 1. ТАБЛИЦА ВАРИАНТОВ
| Вариант | Номера задач | Вариант | Номера задач |
| 7, 26, 69, 82, 101 | 1, 35, 55, 76, 110 | ||
| 14, 29, 54, 89, 104 | 2, 29, 54, 77, 104 | ||
| 20, 33, 59, 95, 108 | 3, 26, 51, 78, 101 | ||
| 9, 43, 67, 1, 118 | 4, 30, 56, 79, 105 | ||
| 12, 37, 65, 87, 112 | 11, 31, 52, 86, 106 | ||
| 10, 30, 58, 85, 105 | 9, 33, 74, 84, 108 | ||
| 19, 39, 68, 94, 114 | 7, 34, 53, 82, 109 | ||
| 11, 34, 60, 86, 109 | 8, 27, 57, 83, 102 | ||
| 15, 28, 64, 90, 103 | 5, 35, 58, 80, 110 | ||
| 2, 27, 53, 77, 102 | 23, 48, 73, 98, 123 | ||
| 4, 41, 52, 79, 116 | 25, 49, 72, 100, 124 | ||
| 18, 47, 51, 93, 122 | 6, 43, 67, 81, 118 | ||
| 5, 45, 66, 80, 120 | 10, 47, 71, 85, 122 | ||
| 21, 49, 62, 96, 124 | 12, 28, 53, 87, 103 | ||
| 25, 35, 61, 100, 110 | 24, 30, 56, 99, 105 | ||
| 17, 40, 56, 92, 115 | 22, 32, 57, 97, 107 | ||
| 8, 50, 63, 83, 125 | 13, 38, 63, 88, 113 | ||
| 23, 44, 71, 98, 119 | 23, 37, 64, 98, 112 | ||
| 1, 31, 55,76,106 | 14, 39, 65, 89, 114 | ||
| 6, 42, 70, 81, 117 | 22, 41, 66, 97, 116 | ||
| 3, 46, 74, 78, 121 | 21, 43, 68, 96, 118 | ||
| 22, 48, 73, 97, 123 | 15, 44, 67, 90, 119 | ||
| 13, 38, 75, 88, 113 | 20, 42, 69, 95, 117 | ||
| 24, 36, 72, 99, 111 | 19, 45, 70, 94, 120 | ||
| 16, 32, 57, 91, 107 | 18, 46, 71, 93, 121 | ||
| 4, 34, 68, 79, 109 | 7, 48, 69, 82, 123 | ||
| 2, 39, 58, 77, 114 | 1, 39, 54, 76, 114 | ||
| 15, 35, 65, 90, 110 | 3, 26, 68, 78, 101 | ||
| 11, 37, 67, 86,112 | 24, 34, 70, 99, 109 | ||
| 19, 43, 59, 94, 118 | 2, 40, 55, 77, 115 | ||
| 10, 33, 54, 85, 108 | 21, 31, 51, 96, 106 | ||
| 7, 43, 65, 82, 118 | 11, 35, 65, 86, 110 | ||
| 14, 34,64, 89, 109 | 17, 44, 59, 92, 119 | ||
| 1, 38, 72, 76, 113 | 5, 50, 75, 80, 125 | ||
| 6, 36, 57, 81, 111 | 23, 38, 58, 98, 113 | ||
| 23, 46, 74, 98, 121 | 12, 28, 53, 87, 103 | ||
| 16, 29, 75, 91, 104 | 8, 40, 63, 83, 115 | ||
| 24, 29, 59, 99, 104 | 10, 42, 52, 85, 117 | ||
| 21, 47, 53, 96, 122 | 6, 39, 53, 81, 114 | ||
| 18, 28, 60, 93, 103 | 16, 32, 57, 81, 107 | ||
| 3, 31, 63, 78, 106 | 13, 45, 60, 88, 120 | ||
| 5, 41, 51, 80, 116 | 14, 26, 56, 89, 101 | ||
| 8, 44, 70, 83, 119 | 22, 37, 62, 97, 112 | ||
| 9, 39, 74, 84, 114 | 4, 43, 61, 79, 118 | ||
| 12, 32, 75, 87, 107 | 18, 37, 56, 93, 112 | ||
| 1, 26, 51, 76, 101 | 20, 36, 67, 95, 111 | ||
| 5, 30, 55, 80, 105 | 15, 27, 66, 90, 102 | ||
| 4, 29, 54, 79, 104 | 9, 50, 71, 84, 125 | ||
| 8, 33, 63, 83, 108 | 19, 49, 58, 94, 124 | ||
| 25, 50, 75, 100, 125 | 25, 34, 74, 100, 109 |
Не нашли, что искали? Воспользуйтесь поиском: