
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Схема емкостного датчика

1 – сварной корпус, 2 – стеклянная труба, 3 – электрод, 4 – регулятор длины электрода (шток), 5 – штурвал, 6 и 10 – верхний и нижний фланцы соответственно, 7 – стальная труба, 8 – кольцо для крепления стеклянной трубы, 9 – металлический цилиндрик.
На верхнем фланце 6 монтируется внутренний электрод 3, особенностью которого является наличие регулятора его длины, действующего при помощи вращающегося штока. Роль изолятора выполняет стеклянная труба 2, которая при помощи специального кольца 8 и стального патрубка 7 крепится к верхнему фланцу 6. Внутри стеклянной трубы на длине 200 мм наносится распылением слой серебра, являющегося внутренним электродом 3 датчика. Вращая штурвал 5 вместе со штоком, можно выдвигать из электрода на требуемую длину металлический цилиндрик 9, контактирующий с серебряным покрытием, таким образом, настраивать влагомер на измерение различных сортов нефти с различной обводненностью. Шкала влагомера, находящаяся на верхнем фланце, отрегулирована в процентах объемного содержания воды. На точность измерения этим прибором количества пластовой воды и нефти значительное влияние оказывают:
1) изменение температуры нефтеводяной смеси;
2) степень однородности смеси;
3) содержание пузырьков газа в потоке жидкости;
4) напряженность электрического поля в датчике.
6. Классификация промысловых трубопроводов. Гидравлический расчет простых трубопроводов.
Трубопроводы, применяемые на нефтяных месторождениях, подразделяются на несколько видов:
1. по назначению – нефтепроводы, газопроводы, нефтегазопроводы, водопроводы. В нефтепроводах и нефтегазопроводах наряду с нефтью и газом может двигаться и пластовая вода.
2. по функции - выкидные линии и коллекторы. Выкидные линии-трубопроводы от устья скважины до ГЗУ. Коллекторы-трубопроводы, собирающие продукцию скважин от групповых установок к сборным пунктам.
3. по величине рабочего давления – низкого (до 1,6МПа), среднего (от 1,6 до 2,5 МПа) и высокого (выше 2,5МПа).
Трубопроводы среднего и высокого давления – напорные. Трубопроводы низкого давления могут быть напорными и самотечными.
Если в самотечных трубопроводах движение жидкости происходит при полном заполнении ею объема трубы, то движение напорно-самотечное, если заполнение не полное, то движение характеризуется как свободно-самотечное.
4. по гидравлической схеме работы - простые и сложные.
Простые - трубопроводы, имеющие неизменный диаметр и массовый расход транспортируемой среды по всей длине.
Сложные - трубопроводы, имеющие различные ответвления или изменяющийся по длине диаметр. Сложные трубопроводы можно разбить на участки, каждый из которых является простым трубопроводом.
5. По способам прокладки:
-подземные,
- наземные,
- подводные,
-подвесные.
Гидравлический расчет простых трубопроводов.
Простой трубопровод имеет постоянный диаметр по всей длине и не имеет никаких отводов. Гидравлический расчет его сводится к определению одного из следующих параметров.
Пропускная способность трубопровода Q при заданных величинах: диаметра D и длины l трубопровода, физических свойств перекачиваемой жидкости (r ж и v ж), геометрических отметках начала и конца трубопровода (D z = z 1 - z 2) и перепада давления (р 1 - р 2) или напора (Н 1 - Н 2).
Необходимый начальный напор Н1 или давление р1 при заданных величинах: конечного напора H 2 или давления p 2, длины трубопровода l, физических свойств перекачиваемой жидкости (r ж и v ж), диаметра трубопровода D, разности геометрических высот D z и количества перекачиваемой жидкости Q ж.
Диаметр трубопровода D, способного пропустить заданный расход Q ж при тех же известных, что и в первых двух случаях.
Рассмотрим принципы решения перечисленных задач.
В задачах первого типа искомым является пропускная способность Q ж трубопровода. Коэффициент гидравлического сопротивления l зависит от числа Рейнольдса, а следовательно, и от неизвестного расхода Q ж. Поэтому задачу решают графо-аналитическим методом, сущность которого сводится к следующему.
В начале задаются несколькими произвольными значениями расхода жидкости Qi, после чего определяют скорость потока  . Затем рассчитывают режим движения
. Затем рассчитывают режим движения 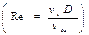 и в зависимости от него определяют коэффициент гидравлического сопротивления l. После чего, подставляя все известные данные в формулу Дарси-Вейсбаха
и в зависимости от него определяют коэффициент гидравлического сопротивления l. После чего, подставляя все известные данные в формулу Дарси-Вейсбаха 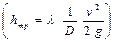 , находят для данного расхода потери напора в трубопроводе Hi и строят по найденным величинам зависимость Hi = f (Qi) (рис.1, а). После этого по заданному напору H 0 находят искомую производительность трубопровода Q 0. При решении этой задачи за заданный напор Н 0, определяемый из уравнения Бернулли обычно принимают разность значений удельной потенциальной энергии (D z и D р):
, находят для данного расхода потери напора в трубопроводе Hi и строят по найденным величинам зависимость Hi = f (Qi) (рис.1, а). После этого по заданному напору H 0 находят искомую производительность трубопровода Q 0. При решении этой задачи за заданный напор Н 0, определяемый из уравнения Бернулли обычно принимают разность значений удельной потенциальной энергии (D z и D р):
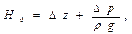
В задачах второго типа в зависимости от числа Рейнольдса, которое в данном случае легко определить по известным диаметру трубопровода D и расходу жидкости Q ж, находят коэффициент гидравлического сопротивления l, затем решают уравнение 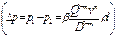 -формула Лейбензона (*) - относительно искомого начального давления.
-формула Лейбензона (*) - относительно искомого начального давления.
В задачах третьего типа искомым является диаметр нефтепровода при известном расходе жидкости Q ж, перепаде давлений p 1 - р 2, плотности r ж и вязкости v ж жидкости, а также длине трубопровода l.
Здесь, как и в задаче первого типа, коэффициент гидравлического сопротивления l зависит как от режима движения, т. е. от числа Рейнольдса, так и от неизвестного диаметра D, входящего в число Re. Поэтому данная задача решается графо-аналитическим методом. Для этого задаются различными значениями диаметра трубопровода Di, определяют соответствующие им потери Hi и строят зависимость Hi = f (Di).
Необходимый диаметр трубопровода определяют по кривой рис. 1 по заданному напору H 0.

7. Классификация промысловых трубопроводов. Гидравлический расчет сложных трубопроводов. Расчет сборного и раздаточного коллекторов.
Трубопроводы, применяемые на нефтяных месторождениях, подразделяются на несколько видов:
1. по назначению – нефтепроводы, газопроводы, нефтегазопроводы, водопроводы. В нефтепроводах и нефтегазопроводах наряду с нефтью и газом может двигаться и пластовая вода.
2. по функции - выкидные линии и коллекторы. Выкидные линии-трубопроводы от устья скважины до ГЗУ. Коллекторы-трубопроводы, собирающие продукцию скважин от групповых установок к сборным пунктам.
3. по величине рабочего давления – низкого (до 1,6МПа), среднего (от 1,6 до 2,5 МПа) и высокого (выше 2,5МПа).
Трубопроводы среднего и высокого давления – напорные. Трубопроводы низкого давления могут быть напорными и самотечными.
Если в самотечных трубопроводах движение жидкости происходит при полном заполнении ею объема трубы, то движение напорно-самотечное, если заполнение не полное, то движение характеризуется как свободно-самотечное.
4. по гидравлической схеме работы - простые и сложные.
Простые - трубопроводы, имеющие неизменный диаметр и массовый расход транспортируемой среды по всей длине.
Сложные - трубопроводы, имеющие различные ответвления или изменяющийся по длине диаметр. Сложные трубопроводы можно разбить на участки, каждый из которых является простым трубопроводом.
5. По способам прокладки:
-подземные,
- наземные,
- подводные,
-подвесные.
Сложный трубопровод может иметь различные диаметры по длине и отводы.
При гидравлическом расчете их практический интерес представляет четыре случая, часто встречающихся в промысловых условиях:
1) жидкость из раздаточного коллектора, имеющего постоянный диаметр, равномерно или неравномерно отбирается;
2) жидкость равномерно или неравномерно поступает в сборный коллектор, имеющий по длине разный диаметр;
3) общий сборный коллектор образует параллельные трубопроводы (лупинги);
4) общий сборный (раздаточный) коллектор имеет форму кольца (магистральный водовод).
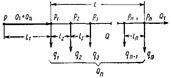
Рассмотрим решение задач для каждого случая при условии установившегося течения.
Уравнение материального баланса для первого случая (см. рис.1) - раздаточного коллектора

где Q - объемный расход жидкости в произвольном сечении; Q T - транзитный расход жидкости, т. е. расход, который транспортируется за пределы указанных участков; Q П - путевой расход жидкости; q 1, q 2, …., qi - равные или неравные объемные расходы жидкости в ответвлениях, отстоящих на расстоянии l 1, l 2, …., li от начала трубопровода.
Расход жидкости на участках:
l1 = О T + Q П;
l2 = О T + Q П - q 1;
l3 = О T + Q П - (q 1 + q 2);
ln = О T + Q П - (q 1 + q 2 + ….. + qn - 1).
Поскольку диаметр раздаточного коллектора одинаков на всем протяжении, а расходы жидкости на различных участках, в связи с ее отбором, разные, то режимы течения на каждом участке l 1, l 2, …., l П также будут разными.
Определим перепад давления на каждом участке горизонтального трубопровода по формуле Лейбензона 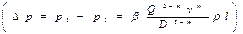 . На первом участке
. На первом участке
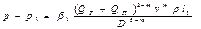
На втором участке
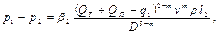
На третьем участке
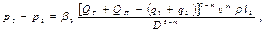
на n -м участке

Сложив перепады на каждом участке, найдем общий перепад на всей длине рассматриваемого раздаточного коллектора:
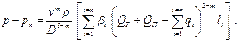
Если транзитный расход в раздаточном коллекторе равен нулю, т. е. Q T = 0, величины отборов одинаковы (q 1 = q 2 = q 3 = ….. qn), расстояния между отборами равны между собой (l 1 = l 2 = …. Ln), то
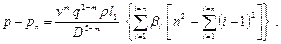
С учетом рельефа местности формула примет вид

Для каждого участка трубопровода определяется режим движения жидкости и по формуле 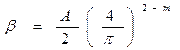
Уравнение материального баланса для второго случая - сборного коллектора
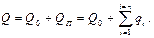
Расход жидкости на участках
l1 = О 0;
l2 = О 0 + q 1;
l3 = О 0 + q 1 + q 2 и т. д.
Определим перепад давления на каждом участке по аналогии с предыдущим.
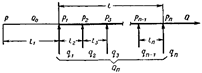
Рис. 2. Расчетная схема сложного нефтепровода, имеющего по длине разные диаметры, с сосредоточенным поступлением нефти
На первом участке

На втором участке
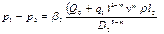
На третьем участке
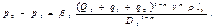
На n -м участке
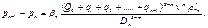
Как и в первом случае, сложив перепады давлений на каждом участке, найдем общий перепад на всей длине рассматриваемого сборного коллектора:

Для каждого участка сборного коллектора определяют режим движения жидкости и определяют перепад давления на каждом участке. Затем производится сложение этих перепадов, в результате чего получается общий перепад.Расчет параллельных и кольцевых трубопроводов.
Сложный трубопровод может иметь различные диаметры по длине и отводы.При гидравлическом расчете их практический интерес представляет четыре случая, часто встречающихся в промысловых условиях:
1) жидкость из раздаточного коллектора, имеющего постоянный диаметр, равномерно или неравномерно отбирается; 2) жидкость равномерно или неравномерно поступает в сборный коллектор, имеющий по длине разный диаметр; 3) общий сборный коллектор образует параллельные ТП (лупинги); 4) общий сборный (раздаточный) коллектор имеет форму кольца (магистральный водовод).
Параллельные ТП, или лупинги, прокладывают обычно для увеличения их пропускной способности при сохранении того же перепада давления на конечных участках или уменьшении его.

Рис. 3. Расчетная схема параллельных трубопроводов (с лупингом)
На рис. 3 приведена схема трубопровода с лупингом.
Из баланса количества жидкости имеем
 где Q 0 - расход жидкости в основном трубопроводе до сечения А и после сечения В; Q 1 - расход жидкости в трубопроводе на участке АВ; Q 2 - расход жидкости в лупинге.
где Q 0 - расход жидкости в основном трубопроводе до сечения А и после сечения В; Q 1 - расход жидкости в трубопроводе на участке АВ; Q 2 - расход жидкости в лупинге.
Очевидно, потери напора на участке трубопровода АВ равны потери напора в лупинге (параллельной трубе), т. е. D h 1 = D h 2 или, можем записать:
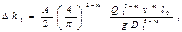

где l 0 - длина участка трубопровода, равная длине лупинга; D 1, D 2 - диаметры трубопровода и лупинга соответственно.
Из равенства потерь напора на участке трубопровода А - В следует
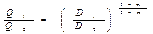
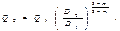
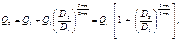
откуда найдем расход в трубопроводе Q 1 на участке AВ, выраженный через расход Q 0 до разветвления:

Формула (7) позволяет определить расход жидкости в сдвоенном трубопроводе по известному суммарному расходу Q 0 и заданным отношениям диаметров лупинга и трубопровода.
Гидравлический уклон до участка АВ и после него
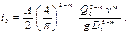
Гидравлический уклон на участке АВ и в лупинге одинаков и будет равен с учетом выражения (7)

Выражая гидравлический уклон на сдвоенном участке через гидравлический уклон основного трубопровода, получим
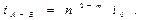
Если диаметр основного трубопровода D 1 и диаметр лупинга D 2 равны между собой, то
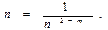
В этом случае при ламинарном режиме n = 0,5, при турбулентном режиме в зоне справедливой для формулы Блазиуса n = 0,297, для зоны с квадратичной характеристикой n = 0,25.
Кольцевые трубопроводы сравнительно широко применяют в промысловых условиях при подаче воды от мест водозабора до кустовых насосных станций (КНС).
Кольцевые трубопроводы рассчитывают по той же схеме, что и при параллельном соединении (с лупингом).
Однако задача значительно усложняется тем, что здесь имеется несколько расходных пунктов Q 1, Q 2, Q 3, Q 4, Q 5 (рис. 4), и расчет проводят до тех пор, пока изменением расхода жидкости и направлением ее движения не будет достигнуто равенство потерь напора в ветвях ВСДЕ и ВМКЕ.
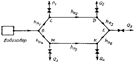
Рис. 4. Расчетная схема кольцевого трубопровода
При проектировании кольцевой системы водоводов вначале задаются величинами расходов Q 1, Q 2, Q 3, Q 4, Q 5 и, зная диаметры отдельных ветвей, определяют значения потерь напора от общей точки разветвления В до расходных пунктов СDЕ и МКЕ. Расходы считаются заданными правильно, если алгебраическая сумма потерь напора в кольце равна нулю, т. е.
 или
или
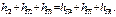
Если это условие не соблюдается, то следует повторить расчеты при измененных величинах расходов жидкости в трубах:
Q 1 + Q 2 + Q 5 = Q 3 + Q 4 + Q 5 ± D Q.
Поправка D Q при этом выбирается удовлетворяющей уравнению

Если в процессе эксплуатации кольцевого трубопровода на линиях-отводах Q 1, Q 2, Q 3, Q 4 и Q 5 изменяется сопротивление (закрывается задвижка), то соответственно этому сопротивлению происходит перераспределение расходов жидкости в отдельных отводах.
8.Неизотермическое течение жидкостей в трубопроводе. Расчет трубопроводов при неизотермическом течении жидкости
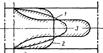 1 – изотермическое ламинарное течение; 2 – нагревание вязкой нефти; 3 – охлаждение вязкой нефти.
1 – изотермическое ламинарное течение; 2 – нагревание вязкой нефти; 3 – охлаждение вязкой нефти.
Закон распределения температуры жидкости по длине трубопровода получен Жуковым в 1883 г., в основу которого заложена  потеря теплоты от элементарного участка dx в единицу времени в ОС:
потеря теплоты от элементарного участка dx в единицу времени в ОС: 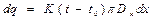 (1), где
(1), где  - поверхность охлаждения элементарного участка, м3,
- поверхность охлаждения элементарного участка, м3, 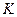 - полный коэффициент теплоотдачи от жидкости в ОС, Вт/м2*0С, t – текущая температура жидкости.
- полный коэффициент теплоотдачи от жидкости в ОС, Вт/м2*0С, t – текущая температура жидкости.
При движении жидкости через рассматриваемый участок dx, жидкость охлаждается на dt 0С и теряет количество теплоты: 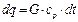 (2), где
(2), где  - теплоемкость, Дж/кг*0С, G – массовый расход, кг/с. (1)=(2):
- теплоемкость, Дж/кг*0С, G – массовый расход, кг/с. (1)=(2): 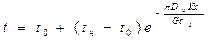 - уравнение Шухова (закон распределения температуры жидкости по длине трубопровода).
- уравнение Шухова (закон распределения температуры жидкости по длине трубопровода).
В 1923 г. Лейбензон внес поправку в эту формулу, учтя работу трения потока жидкости, превращающуюся в теплоту, участвующую в тепловом балансе трубопровода:  ;
; 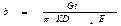 - поправка Лейбензона,
- поправка Лейбензона, 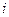 - средний гидравлический уклон; Е – механический эквивалент теплоты (1 ккал=427 кгс*м=427*9,81 Н*м).
- средний гидравлический уклон; Е – механический эквивалент теплоты (1 ккал=427 кгс*м=427*9,81 Н*м).
Закон изменения температуры на участке трубопровода, где происходит кристаллизация парафина, описывается формулой Черникина: 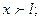
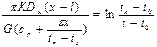 ;
;  - расстояние, на котором температура падает от tн до tп,
- расстояние, на котором температура падает от tн до tп, 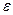 - количество парафина, выделяющегося из нефти при понижении температуры от tп до t
- количество парафина, выделяющегося из нефти при понижении температуры от tп до t 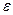 (доли единицы);
(доли единицы); 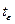 - любая температура, для которой известно
- любая температура, для которой известно 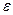 ; x – скрытая теплота кристаллизации парафина.
; x – скрытая теплота кристаллизации парафина.
9.Гидравлический расчет трубопроводов, транспортирующих вязкопластичные жидкости.

распределение скоростей и напряжений в структурированном потоке.
Согласно закону Ньютона о вязкостном трении при движении жидкости в круглой трубе, уравнение касательного напряжения сдвига t записывается в следующем виде:
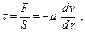
Парафинистые и застывающие нефти при понижении температуры приобретают вязкопластичные свойства вследствие образования в них пространственной структуры. В этом случае течение нефтей не начнется до тех пор, пока не будет достигнуто предельное напряжение сдвига, необходимое для разрушения пространственной структуры, и только после начала течения наблюдается пропорциональность между градиентом скорости и разностью напряжения τ-τ0.
Таким образом, поведение вязкопластичных жидкостей отклоняется от закона Ньютона и описывается уравнением Шведова-Бингама: τ= τ0+μпл 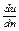 , где τ0-предельное напряжение сдвига, μпл-пластичная вязкость; du/dn-градиент скорости сдвига.
, где τ0-предельное напряжение сдвига, μпл-пластичная вязкость; du/dn-градиент скорости сдвига.
Профиль скоростей при движении вязкопластичной жидкости в круглой трубе существенно отличается от профиля скорости ньютоновской жидкости. Так как напряжение сдвига убывает от стенки трубы и оси, на некотором радиусе r0 напряжение сдвига становится равным предельному напряжению сдвига τ0, и жидкость в цилиндре радиусом r0 движется в виде «ядра», внутри которого скорость по сечению не изменяется. Радиус цилиндрического ядра r0 определяют по формуле: r0 = τ0 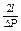 . При ламинарном течении вязкопластичных жидкостей в трубах расход определяют по уравнению Букингема:
. При ламинарном течении вязкопластичных жидкостей в трубах расход определяют по уравнению Букингема:
 ,
,
которое также можно записать
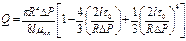 .
.
Для упрощения расчетов применяют формулу Стокса: λ=64/Re*, где Re* - обобщенный параметр Рейнольдса, который вводится с использованием уравнения Букингема в виде: 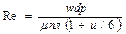 ,
,
где u-параметр пластичности,
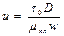 .
.
При турбулентном движении парафинистых нефтей, являющихся вязкопластичными жидкостями, λ не зависит от Re. Численное значение λ в турбулентном режиме в зависимости от содержания парафина изменяется от 0,028 до 0,038, причем λ возрастает с ростом концентрации твердого парафина.
10.Гидравлический расчет трубопроводов для нефтяных эмульсий
Устойчивые высокодисперсные эмульсии ведут себя как однородные жидкости, и поэтому гидравлический расчет трубопроводов в этом случае не отличается от гидравлического расчета простого нефтепровода. Различие гидродинамического поведения неустойчивых и устойчивых эмульсий проявляется в эффекте гашения турбулентных пульсаций дисперсионной среды каплями дисперсной фазы. С учетом этого эффекта λ неустойчивых эмульсий определяется:
λэ=64/Re*э,Re<=2320,
 ,
,
2320< Re*э<105,
где Re*э-число Рейнольдса, определяемое по формуле:
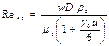 ,
,
где γ0 указывает, является ли неустойчивая эмульсия ньютоновской или неньютоновской жидкостью, ее определяют по выражению:
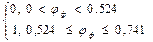 ,
,
1-ньютоновская
2- неньютоновская
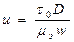 -параметр пластичности,
-параметр пластичности,
w-средняя скорость течения, ρэ, μэ-плотность и вязкость эмульсии; D-внутренний диаметр трубопроводада; τ0- дополнительное напряжение сдвига плотной эмульсии: τ0=(0,195φф-0,102)σ/d, где σ-межфазное натяжение; d-диаметр капель; φф-содержание дисперсной фазы и эмульсии.
Плотная (устойчивая) эм-ия сущ-т при 0,524<φф<0,741
Множитель (1+1,125*γ1 *φф)-1 учитывает эффект гашения турбулентности.
Символ γ1 указывает, проявляется ли в потоке неустойчивой эмульсии эффект гашения турбулентности, и определяется:
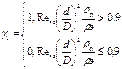 ,
,
где d-средний объемно-поверхностный диаметр капель неустойчивой эмульсии; d=1,4Dwe0.6; We=σ/ρс число Вебера; ρс и ρф-плотность дисперсной среды и дисперсной фазы.
Снижение давления при преодолении гидродинамического сопротивления при турбулентном течении неустойчивых эмульсий в промысловых трубопроводах зависит от содержания дисперсной фазы в неустойчивой эмульсии.
Содержание дисперсной фазы в эмульсии, при котором потери давления будут минимальны, является оптимальным.
1) Потери Р минимальны.
Оптимальное содержание дисперсной фазы в неустойчивой эмульсии определяют по формуле:
φф0=0,68-0,4ρф/ρс, 0,6< ρф<1.4.
2) Потери Р для эм-ии не превышают потерь Р для нефти.
Важное значение для нефтепромысловой практики имеет определение области, в которой перепад давления при течении эмульсии не превышает перепада давления при течении нефти с той же скоростью. Эта область при 1< ρф/ ρc<1.4 описывается формулой: φф*=1,2-0,7 ρф/ ρс.
3) Потери Р для эм-ии меньше чем потери Р для нефти.
Т.о., при 0< φф< φф* перепад давления в труб-де меньше, чем для чистой нефти. За пределами этой области перепад давления для эмульсии превышает перепад давления для чистой нефти.
Не нашли, что искали? Воспользуйтесь поиском: