Основные определения и соотношения

Метод, который предлагается для решения поставленной задачи, базируется на идее распределения степеней принадлежности элементов универсального множества согласно с их рангами. Эта идея раньше использовалась в теории структурного анализа систем, где рассмотрены разные способы определения рангов элементов. Методика распределения надежности по элементам системы согласно их рангов приведена в книге [27].

В нашем случае под рангом элемента будем понимать число , которое характеризует значимость этого элемента в формировании свойства, которое описывается нечетким термом . Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.

В дальнейшем введем такие обозначения:

, , .

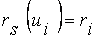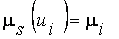Тогда правило распределения степеней принадлежности можно задать в виде соотношения:

(7.7)

до которого прибавляется условие нормирования:

(7.8)

Используя соотношение (7.7), легко определить степени принадлежности всех элементов универсального множества через степень принадлежности опорного элемента.

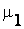Если опорным является элемент с принадлежностью то

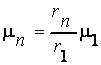, ,..., . (7.9)

Для опорного элемента 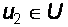принадлежностью получаем:

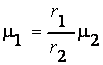, ,..., . (7.10)

И наконец, для опорного элемента с принадлежностью имеем:

,..., . (7.11)

Учитывая условие нормировки (7.8), из соотношений (7.9) - (7.11) находим:

(7.12)

Полученные формулы (7.12) дают возможность вычислять степени принадлежности элементов к нечеткому терму двумя независимыми путями:

1) по абсолютным оценкам уровней , , которые определяются согласно методикам, предложенных в теории структурного анализа систем [17,27]. Для экспертных оценок рангов можно использовать 9-ти бальную шкалу (1 - наименьший ранг, 9 - наибольший ранг) или принцип термометра, который рассмотрен в главе 2.

2) по относительным оценкам рангов , , которые образуют матрицу:

(7.13)

Эта матрица обладает следующими свойствами:

а) она диагональная, т. е. , .

б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: .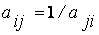

в) она транзитивна, т. е. 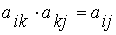, поскольку .

Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы 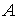легко определить элементы всех других строк. Если известная 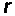-я строка, т. е. элементы , , то произвольный элемент находится так:

, .

Поскольку матрица (7.13) может быть интерпретирована как матрица парных сравнений рангов, то для экспертных оценок элементов этой матрицы можно использовать 9-ти бальную шкалу Саати: В нашем случае эта шкала формируется так:

1 - при отсутствии преимущества над ;

3 -при слабом преимуществе над ;

5 -при существенном преимуществе над ;

7 -при явном преимуществе над ;

9-при абсолютном преимуществе над ;

2,4,6,8 - промежуточные сравнительные оценки.

Таким образом, с помощью полученных формул (7.12), экспертные знания о рангах элементов или их парные сравнения преобразуются в функцию принадлежности нечеткого терма.

Не нашли, что искали? Воспользуйтесь поиском: