Принцип слияния целей и ограничений

В общепринятом подходе главными элементами процесса принятия решения являются: а) множество альтернатив; б) множество ограничений, которые необходимо учитывать при выборе между различными альтернативами и в) функция предпочтительности, ставящая каждой альтернативе в соответствие выигрыш (или проигрыш), который будет получен в результате выбора этой альтернативы.

При рассмотрении этого процесса с более общих позиций принятия решений в нечётких условиях естественной представляется другая логическая схема, важнейшей чертой которой является симметрия по отношению к целям и ограничениям. Эта симметрия устраняет различия между целями и ограничениями и позволяет довольно просто сформировать на их основе решение.

7.1.1. Нечёткие цели и ограничения

Пусть - заданное множество альтернатив. Тогда нечёткая цель, или просто цель, будет отождествляться с фиксированным нечётким множеством в . Например, если (действительная прямая), а нечёткая цель формулируется как " должно быть значительно больше 10", то ее можно представить как нечёткое множество в с функцией принадлежности, имеющей, скажем, такой вид:

(7.1)

Аналогично цели " должно быть в окрестности 15" может быть поставлено в соответствие нечёткое множество с функцией принадлежности:

(7.2)

Подобным же образом нечёткое ограничение, или просто ограничение, в пространстве определяется как некоторое расплывчатое множество в . Например, в случае ограничение " должно находится в диапазоне 2-10 " может быть представлено нечётким множеством с функцией принадлежности, скажем, вида:

,

где - положительное число и - четное положительное число, выбираемое так, чтобы передать смысл, в котором следует понимать "приближение" к заданному интервалу.

Важным аспектом приведенных выше определений является то, что и цель и ограничения рассматриваются как нечёткие множества в пространстве альтернатив; это дает возможность не делать между ними различия при формировании решения.

Действительно, предположим, например, что нечёткая цель и нечёткое ограничение заданы следующим образом:

: должно быть значительно больше 10 и

: должно быть в окрестности 15.

[ и задаются соответственно формулами (7.1) и (7.2)]. Заметим, что цель и ограничения соединены между собою союзом "И", причём "И" соответствует пересечению нечётких множеств. Это означает, что в рассматриваемом примере совокупное влияние нечёткой цели и нечёткого ограничения на выбор альтернатив может быть представлено пересечением . Функция принадлежности для пересечения задается соотношением

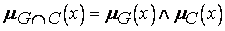
или, в развернутой форме

Отметим, что в силу выпуклости расплывчатых множеств и множество также является выпуклым.

7.1.2. Нечёткие решения

Обратимся теперь к понятию решения. Интуитивно ясно, что решение - это по существу выбор одной или нескольких из имеющихся альтернатив. Предыдущий пример наводит на мысль, что расплывчатое решение, или просто решение, следует определить как нечёткое множество в пространстве альтернатив, получающееся в результате пересечения заданных целей и ограничений. Следующее определение уточняет эту мысль.

Определение 7.1. Пусть в пространстве альтернатив заданы нечёткая цель и нечёткое ограничение . Тогда нечёткое множество , образуемое пересечением и , называется решением. В символической форме

(7.3)

и соответственно . Взаимосвязь между G и C показана на рис.7.1

Рис.7.1. Функции ограничения, цели и решения.

В более общем случае, если имеется целей и ограничений, то результирующее решение определяется пересечением всех заданных целей и ограничений, т.е.

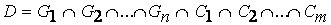(7.4)

и соответственно

(7.5)

Заметим, что в приведенном определении нечёткого решения цели и ограничения входят в выражение для совершенно одинаковым образом, что и соответствует тождественности целей и ограничений в логической схеме процесса принятия решений в нечётких условиях.

Коротко обобщенное определение решения можно сформулировать следующим образом:

Решение = Слияние целей и ограничений.

В качестве иллюстрации к соотношению (7.5) рассмотрим простой пример, в котором , а , , и определяются табл. 7.1. Образуя конъюнкцию , , и , получим таблицу значений для (табл.7.2). Решение в этом случае есть расплывчатое множество

={(2;0,1), (3; 0,4), (4; 0,7), (5; 0,8), (6; 0,6), (7; 0,4), (8; 0,2)}.

Заметим, что ни одно из не принадлежит решению полностью (т.е. со степенью принадлежности, равной 1). Это, конечно, является следствием того, что заданные цели и ограничения вступают в конфликт друг с другом, исключая тем самым возможность существования альтернативы, которая бы полностью им всем удовлетворяла.

Понятие решения как расплывчатого множества в пространстве альтернатив может по началу показаться несколько искусственным. На самом деле оно совершенно естественно, поскольку расплывчатое решение может рассматриваться как некоторая "инструкция", расплывчатость которой является следствием неточности формулировки поставленных целей и ограничений. Так, в приведенном примере , , и могли бы быть выражены следующими фразами: " следует взять близким к 5", " следует взять близким к 3", " следует взять близким к 4", " следует взять близким к 6 ". Тогда решение состоит в том, что " следует взять " " близкое к 5 ". При этом точное значение слова " близко " определяется в каждом случае значением соответствующей функции принадлежности.

Таблица 7.1.

Определение нечётких целей и ограничений

		0.1	0.4	0.8	1.0	0.7	0.4	0.2
	0.1	0.6	1.0	0.9	0.8	0.6	0.5	0.3
	0.3	0.6	0.9	1.0	0.8	0.7	0.5	0.3	0.2	0.1
	0.2	0.4	0.6	0.7	0.9	1.0	0.8	0.6	0.4	0.2

Таблица 7.2.

Определение нечёткого решения

		0,1	0,4	0,7	0,8	0,6	0,4	0,2

Как следует выполнять расплывчатые инструкции типа " следует взять близким к 5 "? Хотя на вопросы такого типа не представляется возможным дать универсальный ответ, во многих случаях все же разумно выбрать те альтернативы, которые имеют максимальную степень принадлежности к . В нашем примере этому соответствует .

В определении нечёткого решения как пересечения или, в более общем смысле, как слияния цели и ограничений подразумевается, что все входящие в цели и ограничения имеют в некотором смысле одинаковую важность. Однако встречаются ситуации, в которых некоторые цели и, возможно, некоторые ограничения являются более важными, чем остальные. В таких случаях решение может быть выражено выпуклой комбинацией целей и ограничений с весовыми коэффициентами, характеризующими относительную важность составляющих элементов. Таким образом, может быть записано в виде:

(7.6)

где и - функции принадлежности, такие, что

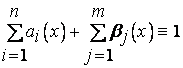
С учетом этого ограничения и могут быть подобраны так, чтобы передавать относительную важность целей 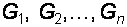и ограничений . В частности, если , получится любое расплывчатое множество, содержащееся в и включающее . Отметим, что формула (7.6) напоминает известный способ сведения векторного критерия к скалярному с помощью образования линейной комбинации компонент векторной функции цели.

Не нашли, что искали? Воспользуйтесь поиском: