
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Настройка модели прогнозирования
Задача настройки состоит в подборе таких параметров и функций принадлежности лингвистических оценок (рис. 8.12), которые обеспечат минимум расхождения между теоретическим и экспериментальным количеством заболеваний. В соответствии с методом наименьших квадратов эта задача формулируется так:
найти такие параметры и, что
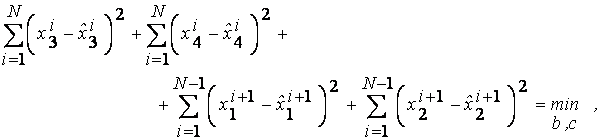
где  ,
, 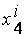 ,
,  ,
,  - прогнозные количества заболеваний, которые зависят от параметров
- прогнозные количества заболеваний, которые зависят от параметров 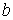 и
и  функций принадлежности,
функций принадлежности,
 ,
,  ,
, 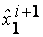 ,
, 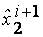 - экспериментальные количества заболеваний,
- экспериментальные количества заболеваний,
 - число циклов, которые используются для настройки модели.
- число циклов, которые используются для настройки модели.
После настройки модели прогнозирования при  , что соответствует использованию данных за 1982 - 1993 годы, получены параметры функций принадлежности, показанные в табл. 8.13.
, что соответствует использованию данных за 1982 - 1993 годы, получены параметры функций принадлежности, показанные в табл. 8.13.
Таблица 8.13.
Параметры функций принадлежности после настройки
| Лингвистические оценки переменных | Параметр | |
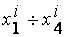
| 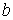
| 
|
| низкая (Н) | 100.385 | 14.148 |
| ниже среднего (нС) | 146.602 | 21.046 |
| средняя (С) | 195.650 | 7.621 |
| выше среднего (вС) | 234.457 | 19.760 |
| высокая (В) | 251.836 | 36.640 |
Задача оптимизации решалась генетическим алгоритмом. Функции принадлежности после настройки приведены на рис. 8.14. В расчет принималось:  ,
,  ,
, 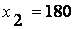 ,
, 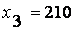 ,
,  ,
,  .
.

Использование настроенных функций принадлежности дает модель прогнозирования, которая достаточно близка к экспериментальным данным (рис. 8.15).
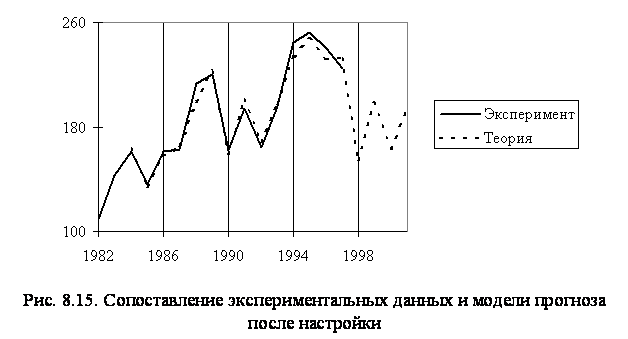
Поскольку экспериментальные значения количества заболеваний в 1994-1997 годах не использовались при настройке модели, то близкие результаты теории и эксперимента в этих годах свидетельствуют о достаточном для практики качестве построенной модели прогнозирования. Ошибка модели прогноза, а также прогноз количества заболеваний аппендикулярным перитонитом до 2001 года представлены в табл. 8.14.
Таблица 8.14.
Экспериментальное и теоретическое количество заболеваний.
| Год | ||||||||||
| Эксперимент | ||||||||||
| Теория | ||||||||||
| Ошибка | ||||||||||
| Год | ||||||||||
| Эксперимент | ||||||||||
| Теория | ||||||||||
| Ошибка |
8.4. Идентификация коэффициента сцепления "автомобиль-дорога"
Задача оценки коэффициента сцепления колес автомобиля с дорожным покрытием возникает в связи с проведением автотехнической экспертизы при расследовании дорожно-транспортных происшествий (ДТП). От точности определения коэффициента сцепления зависит объективность принятия решения о виновности или невиновности водителя, который совершил ДТП (например, наезд на пешехода). Существующая методика позволяет определить только диапазон возможных значений коэффициента сцепления в зависимости от ряда влияющих факторов. Поэтому, окончательная его оценка определяется автотехническим экспертом субъективно, с учетом дополнительных факторов и условий, которые не входят в методику.
Принятие решения о причине аварии очень чувствительно к значению коэффициента сцепления: субъективный выбор нижнего или верхнего значения коэффициента может решить судьбу участников происшествия.
Целью исследования, результаты которого представлены в этом разделе, была разработка математической модели оценки коэффициента сцепления, которая бы учитывала всю доступную информацию о влияющих факторах и, за счет уточнения величины коэффициента сцепления, повышала объективность решений [49,70].
Не нашли, что искали? Воспользуйтесь поиском: