ДЕМОНСТРАЦИЯ ПО АНАЛОГИИ

Уподобления не доказывают, а лишь

объясняют доказанное. M.B. Ломоносов

Очень распространенным типом доказательства является демонстрация по аналогии (греч. analogía — соответствие, сходство). В доказательстве по аналогии обосновывается сходство двух предме­тов в каком-либо признаке на основании того, что эти предметы име­ют ряд других сходных признаков.

Например, для того чтобы доказать идею о возможности существования органической жизни на какой-либо другой планете, ученые рас­суждают так: на данной планете есть атмосфера с наличием в ней кислорода, есть вода, есть необходимая для возникновения жизни температура; на Земле есть такая атмосфера, есть вода, есть требуемая температура и есть органическая жизнь. Поскольку данная планета и Земля сходны в ряде существенных признаков, поэтому, вероятно, они сходны и еще в одном признаке — наличии органической жизни.

Схема доказательства по аналогии такова: пусть некоторый объект А обладает последовательностью свойств а ₁, а ₂ ,..., a_{n +1} —

А: а ₁, а ₂, а ₃, а_n,..., а_{n +1}.

Второй объект В обладает набором свойств, совпадающих со свойствами объекта А, за исключением а_{n +1}, про который ничего не известно, —

B: a ₁ ,a ₂ ,a ₃ ,..., а_n.

Тогда из этих двух наблюдений можно сделать вывод, что и второй объект В обладает свойством а_{n +1} (формула 1).

Доказательство по аналогии основано на том, что предметы могут быть подобными, сходными в каких-либо свойствах, признаках или отношениях, причем такие предметы, которые в целом различны. Умозаключение по аналогии — это логический вывод, в результате которо­го достигается знание о признаках одного предмета на основании зна­ния того, что этот предмет имеет сходство с другими предметами.

Очевидно, что доказательство по аналогии не является абсолютным, оно гипотетическое. Вы только предполагаете, что второй объект об­ладает еще и дополнительным свойством. Не являясь абсолютным, в определенных случаях доказательство по аналогии бывает крайне убе­дительным. Приведем исторический пример доказательства по анало­гии, которое оказалось настолько убедительным, что под это доказа­тельство была выделена очень крупная сумма денег. Человек по имени Гаргреве отправился в Австралию в район, который называется Новый Южный Уэльс, и обнаружил там горные породы, очень напоминающие породы знаменитых калифорнийских гор, которые находятся в США. Калифорнийские горы он хорошо знал, так как неоднократно бывал там и работал. Горы в Калифорнии очень богаты минералами.

Пусть в нашем определении A — это горы в Калифорнии, а В — это горы в Новом Южном Уэльсе. Гаргреве заметил поразительное сход­ство: олово есть и там, и там (а ₁ ), цинк есть и там, и там (а ₂ ), свинец есть и там, и там (a ₃), железная руда есть и там, и там (а ₄), и т.д.

Оценивая признаки, которые оказываются одинаковыми для этих двух горных массивов, он доходит до главного признака, который им не обнаружен, но он подозревает о его существовании. Этот признак a_{n +1} — наличие золота. В горах Калифорнии очень много золота. И он делает предположение, что в Австралии в породе должно быть золо­то. Он возвращается домой, пишет доклад и в этом докладе, предла­гая доказательство по аналогии, аргументирует наличие золота в Австралии. Доклад заканчивается просьбой о выделении очень круп­ной суммы денег на организацию экспедиции для поиска золота. До­казательство сочли убедительным. Деньги были выделены. Экспеди­ция отправилась в Австралию, и золото действительно нашли.

Основоположник кибернетики Н. Винер, приступая к исследова­ниям в области конструирования логических машин, вдохновлялся такой, оказавшейся очень эффективной аналогией. "С самого нача­ла, — пишет он, — я был поражен сходством между принципами дей­ствия нервной системы и цифровых вычислительных машин. Я не со­бираюсь утверждать, что эта аналогия является полной, и мы исчер­паем все свойства нервной системы, уподобив ее цифровым вычисли­тельным устройствам. Я хотел бы только подчеркнуть, что в некото­рых отношениях поведение нервной системы очень близко к тому, что мы наблюдаем в вычислительных устройствах".

О том, какую огромную роль аналогия играет в кибернетике, свидетельствует французский ученый Л. Куффиньяль. Убедившись в аналогичности двух механизмов, показывает он, предполагают, что известные функции одного механизма присущи и другому механизму, для которого их наличие не установлено. Как, например, устанавливают дозы новых лекарств для человека? По аналогии функций организ­мов животного и человека. При изучении действия лекарственного препарата сначала проводят опыты на животных и затем предполага­ют, что при назначении этого лекарства человеку результаты будут аналогичны результатам, полученным в опытах с животными.

Умозаключение по аналогии, как и любое другое умозаключение, является отображением в нашем сознании обычных отношений вещей. Человек на практике многократно наблюдал постоянство и устойчи­вость связей между признаками в предметах и явлениях внешнего мира. С течением времени эти связи признаков вещей зафиксировались в со­знании человека в виде определенной фигуры логики, которая приоб­рела аксиоматический характер. Так, человек давно заметил, что если в двух предметах или явлениях имеются какие-то общие существен­ные признаки, то вполне возможно, несмотря даже на ряд свойственных этим предметам отличительных черт, предполагать, что эти предметы об­ладают также и другими сходными признаками. Если есть корни, ствол и ветки, то, как правило, есть и листья; если тело жидкое, то в любых сообщающихся сосудах оно расположится на одинаковом уровне, хотя бы эти сосуды отличались формой; если тело хорошо проводит тепло, значит, можно ожидать, что оно хорошо проводит и электричество, и т.д.

Эта уверенность имеет и другое основание в окружающем мире: общая закономерность, которая выражается в существенных призна­ках предмета или явления, всегда встречается в связи с рядом одних и тех же постоянных устойчивых признаков, хотя условия, в которых проявляется данная общая закономерность, могут быть различными.

Привычка нашего ума к аналогии настолько сильна, что она иног­да начинает действовать как бы механически. Аналогия, как мы уже видели, основана на том, что сходные в одном отношении вещи сходны и в остальном. Привыкнув к этому, люди удивляются, что шерстяные одеяла употребляются для предохранения льда от таяния, тогда как обычно шерстяные одеяла применяются для сохранения тепла.

Такой вид аналогии часто встречается в практике самых различ­ных ученых и специалистов. Так, ботаник, замечая по некоторым при­знакам сходство какого-либо растения с известными ему представите­лями вида, относит данное растение к этому виду, предполагая, что в найденном растении есть все, еще и не исследованные видовые призна­ки. Говоря об аналогии, можно сослаться на ряд примеров из истории науки: на аналогию Ньютона между падением яблока и движением не­бесных тел, на аналогию Франклина между электрической искрой и молнией, на аналогию между распространением волн на воде и звука в воздухе и пр.

Ломоносов в одной из своих ранних работ на основании аналогии сделал вывод о том, что свет есть материя. "Один свет, — пишет он, — затемняет другой, например, солнце — свет свечи; подобно тому, как более сильный голос заглушает другой, слабый. Отсюда следует, что свет есть материя". Английский логик Джевонс говорит, что даже жи­вотные "делают заключения" до некоторой степени путем аналогии. Так, битая собака боится каждой палки, и существует очень немного собак, которые не убегут, если вы сделаете вид, будто поднимаете камень, хотя бы на этом месте не было никакого камня. Признание нормальной ана­логии между двумя системами идей, говорит Дж.К. Максвелл, "приво­дит к более глубокому знанию обеих, чем познание, которое можно было получить, изучая каждую систему в отдельности".

Аналогия благодаря своей наглядности и доступности широко используется в математике: а) при изучении десятичных дробей подчеркивается их аналогия с натуральными числами; б) свойства алгебраических дробей аналогичны свойствам арифметических (обыкновенных) дробей; в) методика решения задач на составление уравнений второй степени аналогична методике решения задач на составление уравнений первой степени; г) свойства членов геометрической прогрессии во мно­гом аналогичны свойствам членов арифметической прогрессии и т.п.

Ход умозаключения по этому виду аналогий можно записать в виде следующей формулы:

А имеет признаки а ₁, а ₂, а ₃, х;

В имеет признаки а ₁, а ₂, а ₃;

Вероятно, В имеет и признак х.

Возьмем такой пример: модель самолета (А) имеет такую же форму (а ₁ ), такое же отношение веса к плоскости крыльев (а ₂ ), такое же соотношение между весом носовой части и остальной части фюзеляжа (а ₃), как и конструируемый самолет. При испытании модели в аэродинами­ческой трубе оказывается, что модель неустойчива (x). На основании аналогии (сходство модели и самолета в трех признаках) конструктор непременно сделает вывод, что самолет будет также неустойчив при полете.

Умозаключения по аналогии применяются в физике, строительстве плотин, в лингвистике, кибернетике, истории и т.д. Это, в частности, объясняется тем, что во всех областях науки начинает интенсивно внедряться моделирование, когда возможное поведение интересующих нас объектов исследуется на условных образах, аналогичных исследуемому объекту.

Под моделью (лат. modulus — мера, франц. modèle — образец) в науке понимается искусственно созданный объект в виде схемы, чер­тежа, логико-математических знаковых формул, физической конструк­ции и т.п., который, будучи аналогичен (подобен, сходен) исследуе­мому объекту (самолету, человеческому сознанию, клетке и т.д.), ото­бражает и воспроизводит в более простом, уменьшенном виде струк­туру, свойства, взаимосвязи и отношения между элементами исследу­емого объекта, непосредственное изучение которого невозможно, не­доступно или связано со значительными трудностями, большими зат­ратами средств и энергии, и тем самым облегчает процесс получения информации об интересующем нас предмете.

Исследуемый объект, по отношению к которому строится модель, называется черным ящиком, который представляет собой оригинал, об­разец, прототип, подчас не данный нам в наблюдении.

Все существующие модели обычно подразделяются на три типа: физические, вещественно-математические и логико-математические. Физические модели имеют природу, сходную с природой изуча­емого объекта, и отличаются от него лишь размерами, скоростью тече­ния исследуемых явлений и иногда материалом. Вещественно-ма­тематические модели имеют отличную от прототипов физическую природу, но допускают одинаковое с оригиналом математическое опи­сание. Логико-математические модели конструируются из зна­ков. Это абстрактные модели, которые строятся как исчисления (лат. calculus — счет). Под исчислением понимается, таким образом, систе­ма изучения объектов внешнего мира, в которой предметам какой-либо определенной области ставятся в соответствие материальные знаки (цифры, буквы и др.), и с ними затем по принятым в системе точным правилам производятся операции, необходимые для достижения постав­ленной цели. Исчисление можно определить и как формальное устрой­ство, позволяющее получать одни последовательности символов из дру­гих путем вывода. Исчисления имеют конечный алфавит и правило вывода (С.К. Клини). Математика, возникшая шесть тысячелетий тому назад в Древнем Египте и Вавилонии, строилась прежде всего как исчисление. Только в III в. до н.э. Евклид впервые построил математи­ку в виде аксиоматической теории, т.е. теории, построенной из конеч­ного числа аксиом (греч. axioma — значимое, достойное уважения, при­нятое, бесспорное) — истинных суждений, которые в рамках замкну­той теорий принимаются без доказательств в качестве исходного поло­жения и которые кладутся в основу доказательства всех других поло­жений этой теории. Из аксиом с помощью заданных правил вывода дедуктивно могут быть получены содержательно истинные предложе­ния (теоремы), сформулированные на языке данной теории.

Но до сих пор в современной школе изучение математики начи­нается с нумерации и четырех действий арифметики, т.е. с оперирова­ния знаками (цифрами), что само по себе является исчислением.

В математической логике имеется несколько взаимосвязанных исчислений:

1) исчисление высказываний, изучающее логические операции с простыми высказываниями, которые объединяются в сложные высказывания с помощью логических связок, сходных с принятыми в обычной речи союзами: и (конъюнкция, в математической логике он представлен сим­волом &), или (дизъюнкция, символ V), если... то... (импликация, сим­вол ®), тогда и только тогда, когда (эквивалентность, символ ~), а также с отрицанием, обозначаемым частицей не (символ ù);

2) исчисление классов, изучающее символику Аристотеля;

3) исчисление предикатов, исследующее операции с высказыва­ниями, расчлененными на субъект и предикат;

4) исчисление отношений, исследующее логические свойства и операции над двухместными, трехместными и т.п. отношениями.

Примером модели, построенной как исчисление, может служить модель (или теория) трансформационных порождающих грамматик (ТТПГ), предложенная выдающимся американским лингвистом Н. Хомским. ТТПГ опирается на тот факт, что любой носитель естественного языка может понять подавляющее большинство предложений, которые он никогда не слышал. Следовательно, в мозгу человека существует ус­тройство, которое помогает ему понимать и воспроизводить правиль­ные фразы известного ему языка (языков) и отвергать неверные. Это устройство, как уже говорилось, называется competence и является объек­том изучения лингвистики, так как этот объект сегодняшними сред­ствами естественных наук не может быть изучен. Ставится задача его моделирования. Под языком в ТТПГ понимается множество цепочек из конечного числа элементов. Одни цепочки являются предложения­ми, другие — нет. Основная задача лингвистики определяется как уме­ние отличить грамматически правильные предложения от неправильных и исследовать структуру правильных предложений. Грамматика — это модель устройства, порождающего все правильные фразы данного языка и только их. Порождение — это не построение в мозгу правиль­ной фразы, а перечисление правильных фраз. При этом грамматичность нельзя путать с осмысленностью и вероятностью встречаемости. Так, неправильными считаются предложения типа:

1)Furiously sleep ideas green colorless (англ.)

2) Read you a book on modern music (англ.)

3) Je n'ai vu rien (фр.)

4) Je n'ai personne vu (фр.).

А предложение Green colorless ideas sleep furiosly (Зеленые бесцвет­ные идеи яростно спят) рассматривается как правильное. Грамматич­ными являются предложения, в которых при замене одних членов дру­гими с теми же грамматическими показателями получается правиль­ная фраза. Каждый человек в своей жизни слышал не так уж много предложений, но всегда может отличить правильную фразу от непра­вильной. Лингвист моделирует структуру такого типа на базе конеч­ного числа известных (наблюденных) правильных и неправильных предложений. В качестве примера могут быть рассмотрены следующие правила порождения, предлагаемые в ТТПГ:

(I) S ® NP+ VP (S — предложение, NP— группа существитель­ного, VР — глагольная группа)

(II) NP ® Det +N

(III) VP ® V+ NP

(IV) Det ® the

(V) N ® man, ball...

(VI) V ® hit, took…

С помощью этих правил можно образовать правильную английскую фразу: The man hit the ball ( "Мужчина ударил по мячу"):

S

NP + VP (I)

Det + N + VP (II)

Det + N + V + NP (III)

the + N + V + NP (IV)

the + man + V + NP (V)

the + man + hit + NP (VI)

the + man + hit + Det + N (II)

the + man + hit + the + N (IV)

the + man + hit + the + ball (V)

Предложения типа The man hit the ball называются ядерными, так как являются следствием прямого вывода. Из ядерных предложений по специальным правилам можно получить пассивные, вопросительные фразы и т.д.

Все правила делятся на Р -правила (правила структуры составляю­щих) и T -правила (трансформационные правила).

А ® В (Р- правила: заменить А на В, или А º В, или " A " is " В " );

А Þ В (Т- правила: т.е. В выведено из А).

Р -правила бывают двух видов: контекстно-свободные (context-free) и контекстно-связанные (context-restricted). Правило называется контекстно-связанным, если оно устанавливает, что символ А может быть заменен символом В, только если находится в окружении X — Y, т.е. X предшествует А, a Y непосредственно следует за А:

А ® В / X — Y.

Все остальные правила — контекстно-свободные. Действие P -пра­вил определяется следующими требованиями:

1) каждое правило должно развертывать один символ;

2) каждый развертываемый символ (за исключением начального) должен входить и в правую часть какого-либо правила;

3) ни один символ не может заменяться пустым символом (т.е. опускаться);

4) результирующая цепочка должна быть отлична от начальной, т.е.

А ↛ Х + A + Y;

5) для любой пары символов в грамматике не может одновременно содержаться пара правил: А ® В; В ® А.

ься пара правил: А ® В; В ® А.

Вывод по Р -правилам может быть представлен в виде дерева. Например:

T -правила — это правила подстановки вида А Þ В. Если Р -правила переводят одни цепочки в другие, то T -правила переводят одни дере­вья в другие деревья. T -правила делятся на обязательные (Tob) и фа­культативные (Topt).

Например, Topt: NP+ VP+ Adv Þ Adv+ NP+ VP (факультативно наречие из конца предложения может быть перенесено в начало).

Левая часть трансформации (T -правила) называется структурным описанием (structural description), правая — структурным изменением (structural change), а сама подстановка — операцией. Операции мо­гут быть элементарными или представлять собой комбинацию элемен­тарных операций. Элементарными операциями являются: 1) добавле­ние (addition); 2) опущение (omission); 3) перестановка (permutation); 4) субституция (substitution).

Примеры:

1) X + Y Þ Х+ Y +Z (добавление)

2) X+ Y Þ Y (опущение)

3) Х+ Y+ Z Þ X +Z + Y (перестановка)

4) Х+ В + С Þ X + D + C, где D может быть только терминальным, т.е. конечным символом.

Правила могут комбинироваться. Например:

B + C + D Þ D + C (перестановка и опущение).

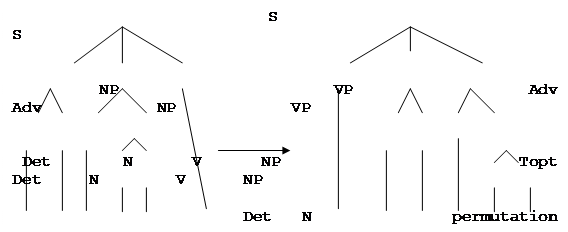
Пример применения трансформационного правила (факультатив­ный перенос наречия в начало предложения, см. рис. ниже).

Правила оперируют с символами, превращая их в цепочки и де­ревья.

Все символы делятся на основные (словарные) и вспомогательные. Словарные символы состоят из символов классов, которые репрезенти­руют составляющие высоких рангов — NP, VP и т.д., и морфемных символов, которые представляют собой составляющие низших рангов — man, hit и т.д. Начальный символ S — sentence (предложение), который относится к основным, задается до первого правила, он определяет гра­ницы порождающей грамматики. Среди морфемных символов разли­чают символы грамматических морфем (морфемы Pres, Past и т.д.) и сим­волы лексических

морфем. Морфемные символы являются конечными, они называются терминальными (лат. termino — ограничивать). Цепоч­ка — это соединение одного или нескольких словарных символов. Вспо­могательные символы делятся на переменные символы, для каждого из которых должна быть задана область его применения (W, У, Z и т.д.), операторы (®, + и т.д.) и символы сокращений, т.е. скобки. Р -правила устанавливают структуры, лежащие в основе языка, а Т -правила из­меняют структуры. Предложение, полученное применением Т -правил, называется производным, или выведенным, предложением (derived sentence). Терминальные цепочки имеют абстрактный вид, обязатель­ные трансформации (Тов) превращают их в предложения языка, гото­вые к фонетической интерпретации. Предложения, полученные в ре­зультате применения Р -правил и обязательных Т -правил (и только их), — называются ядерными предложениями (kernel sentences). Если два предложения выведены посредством Т -правил из одного глубин­ного, их называют родственными (related sentences). Например, род­ственными являются следующие четыре предложения:

1. Mary hit the boy.

2. The boy was hit by Mary.

3. Whom hit Mary?

4. Who hit the boy?

Общая глубинная структура этих предложений следующая:

P -правила всегда предшествуют T -правилам. Оба типа правил строго упорядочены: после применения правила i правило j приме­нять нельзя, если i < j. Одно и то же правило можно применять сколько угодно раз подряд, если сохраняются условия для его применения. Для Р -правил обязательно развертывание нетерминальных символов высших рангов прежде развертывания нетерминальных символов низ­ших рангов, а развертывание нетерминальных символов должно пред­шествовать развертыванию терминальных символов. Эти последствия должны группироваться в конце.

Для T -правил обязательно выполнение следующего требования: более общие правила должны следовать за менее общими, при этом выход одного должен являться входом другого.

Для построения ТТПГ нужен корпус, содержащий: а) список различных максимально грамматичных предложений рассматриваемого языка; б) список различных максимально неграмматичных предложе­ний языка. (Пробную грамматику можно построить уже по первому списку.)

Ключевыми моментами процедуры построения ТТПГ являются:

1. Определение значения морфем и составление словаря вида: мор­фема — ее значение — принадлежность к некоторому классу (напри­мер, к классу суффиксов существительного).

2. Установление того, про какие классы можно сказать, что они образуют субъект и т.п., т.е. установление функций классов, полу­ченных в первом пункте, и выделение типов предложений, объединяе­мых тождественным порядком тождественных функций, например:

субъект — глагол — объект (1-й класс),

субъект — глагол (2-й класс) и т.д.

3. Установление, начиная с самого длинного предложения, и запись в виде таблицы встречаемости классов и позиции этой встречаемости.

4. Установление того, какие элементы встречаются всегда, какие не всегда, какие встречаются вместе и т.п., и сведение таким способом к минимуму число возможных комбинаций и типов.

5. Установление синтаксических отношений между членами в предложениях разных типов.

6. Сравнение типов предложений и изучение их сходства и разли­чия.

7. Запись решения с соблюдением рекомендуемого порядка применения правил.

8. Проверка решения и внесение исправлений.

ТТПГ претендует на статус общей теории, которая объясняет все имеющиеся факты и предсказывает все возможные новые. Объясни­тельные теории считаются высшей ступенью научного описания.

Любая моделирующая теория должна удовлетворять требовани­ям внешней адекватности (в нашем случае — перечислять только пра­вильные предложения) и общности (в ТТПГ общие понятия формули­руются вне зависимости от конкретного языка).

Наука о языке проходит в своем развитии стадии, связанные с тре­мя разными процедурами.

1. Процедура открытия грамматики:

2. Процедура суждения о грамматике:

3. Процедура выбора грамматики:

На долю лингвистической теории выпадает третья процедура. Причем на современном уровне развития науки о языке становится понятно, что разные грамматики (т.е. разные модели, разные описа­ния) одновременно могут быть признаны удовлетворительными, а их выбор связан с конкретной целью, для которой данная модель строи­лась, т.е. определяется прагматически (например, G ₁ — грамматика, предназначенная для обучения данному естественному языку иност­ранцев, а G ₂ — грамматика, используемая в программах по автома­тическому переводу).

Любой грамматике как модели должны быть присущи следующие свойства:

1) формальность — апелляция к материальной стороне знака, а не к значению, т.е. опора не на интуицию;

2) эксплицитность — самостоятельная интерпретация всех форм;

3) полнота — покрытие всех фактов языка;

4) простота — использование по возможности меньшего числа символов и обладание максимально обобщенными правилами.

При наличии первых трех свойств четвертое свойство позволяет сравнивать разные грамматики между собой.

По определению Н. Хомского, трансформационная порождающая грамматика языка L — это такое, устройство, находящееся в рамках определенной общелингвистической теории, удовлетворяющее требова­ниям внешней адекватности и общности и обладающее свойствами формальности, эксплицитности, полноты и простоты, которое порождает (т.е. перечисляет) все правильные предложения языка L, приписывает им их структурные описания и не порождает неправильных предло­жений (не предложений).

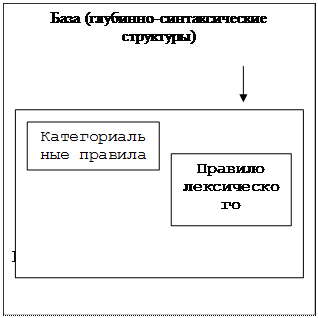
Трансформационная порождающая грамматика, как показано на схеме, состоит из трех компонентов: синтаксического, фонологическо­го и семантического.

Непреходящее значение теории трансформационных порождающих грамматик заключается в том, что фактически — это единственная полноценная попытка создания непротиворечивой модели языковой способности человека, локализованной в мозгу, но являющейся одной из самых недоступных научных тайн — тайной речевого мышления лю­дей!

Схема трансформационной порождающей грамматики

Синтаксический компонент Семантический компонент

Поверхностные структуры

Фонетическая репрезентация

Три типа моделей: физические, вещественно-математические и ло­гико-математические не являются полностью автономными. Так, ло­гико-математические модели можно воплотить в вещественно-матема­тические и даже в физические и наоборот.

Модели могут создаваться как из однородного с оригиналом ма­териала (например, макет деревянной церкви в Кижах тоже был сделан из дерева), так и из материала, совершенно отличного от матери­ала оригинала (например, модель мыслительной операции логик изоб­ражает в виде чертежа на бумаге или дедуктивного построения).

Простейшей формой физической модели является макет. Так, строители плотин, как правило, первоначально изготовляют макет (мо­дель) плотины в уменьшенном размере и на ней производят необходи­мые измерения, изучают движение воды, формы русла, свойства грун­та, водонапорных сооружений и т.п.; архитекторы строят макет дома; авиаконструкторы — модель самолета и т.д.

В формальной логике модели применяются издавна. Так, например, моделью первой фигуры простого категорического силлогизма, нося­щей название Barbara (см. выше), служит следующая схема:

В логике модель выступает, кроме всего прочего, как средство конкретизации, наглядного представления абстрактного. В ней как бы сочетаются в единстве чувственное и логическое.

Логическое моделирование развивалось и в средние века. Испанс­кий философ и богослов Раймунд Луллий попытался смоделировать логические операции с помощью изобретенного им логического круга (первой "логической машины"). В XVIII веке Ч. Стенхоп разработал "демонстратор", который он применял для проверки, в частности, сил­логизмов с количественно определенными предложениями. В XIX веке английский логик У.С. Джевонс построил логическую машину, позво­лившую механизировать ряд процедур в логике классов и в силлогисти­ке. В принципе сегодня открыта возможность моделирования многих умственных процессов, хотя и не создано запоминающих устройств, сравнимых по емкости и эффективности с миллиардами нейронов коры головного мозга. Однако думается, что разработки в сфере искусствен­ного интеллекта a priori ограничены некоторым пределом (см. выше). Сегодня исследования идут по пути моделирования отдельных про­цессов работы мозга и отдельных видов умственного труда, привлекая огромные возможности быстродействующих компьютеров. Моде­лирование все шире начинает применяться в ходе формулирования и проверки гипотез (греч. hypóthesis — основание, предположение) — вероятных предположений о причине каких-либо явлений, достовер­ность которых при современном состоянии производства и науки не может быть проверена и доказана, но которые объясняют данные яв­ления, без них необъяснимые. Гипотеза — прием познавательной деятельности человека.

Остановимся на этой проблеме несколько подробнее. Кроме дан­ного истолкования термина гипотеза, как проблематичного, вероятно­го знания, в логической литературе выделяются еще два значения этого термина: 1) гипотеза в широком смысле слова — как догадка о чем бы то ни было, как описательная гипотеза, которая, как правило, является кратким резюме изученных явлений, описывающим формы их связи; 2) гипотеза в узком смысле слова — как научная гипотеза, которая все­гда выходит за пределы изученного круга фактов, объясняет их и пред­сказывает новые факты; систематизируя знания, научная гипотеза по­зволяет объединить некоторую полученную совокупность информации в систему знаний и образует теорию, если ее предположение подтверж­дается практикой.

В каких же случаях употребляется гипотеза? Она необходима:

1) когда известные факты недостаточны для объяснения причин­ной зависимости явления, а есть надобность в том, чтобы его объяс­нить;

2) когда факты сложны, и гипотеза может принести пользу как обобщение знаний в данный момент, как первый шаг к разъяснению их;

3) когда причины, произведшие или производящие факты, недо­ступны опыту, а между тем действия или следствия их могут быть изу­чаемы.

Значение гипотез в познании окружающего мира огромно. Без ги­потез невозможно развитие современных научных знаний. В процессе производства материальных благ, в ходе научного исследования люди ежедневно открывают десятки и сотни новых фактов и явлений в окружающем их мире. Подавляющее большинство этих новых фак­тов и явлений находит свое объяснение с помощью существующих научных теорий.

Но в жизни нередко бывает так, что то или иное новое явление не поддается истолкованию с помощью существующих уже научных тео­рий, приемов и средств научного исследования. В таких случаях снача­ла выдвигается научное предположение о возможных причинах су­ществования вновь открытого факта или явления природы. Давно, например, было замечено, что с углублением в кору земли через каждые 30—33 метра температура в шахте повышается на 1 градус. На ос­новании этого факта и некоторых других известных явлений (наличие потоков горячей лавы при извержении вулканов, существование горя­чих источников подземных вод и др.) было высказано предположение о том, что внутри земного шара температура достигает многих тысяч градусов. При современном уровне научных знаний и техники дан­ное предположение о температуре внутри земного шара не могло быть доказано путем непосредственного наблюдения. Но, несмотря на это, такое предположение ценно тем, что объясняет ряд природных явлений (повышение температуры Земли с увеличением глубины шахты, высо­кую температуру лавы, изверженной вулканом, и т.д.).

Значение гипотезы в науке высоко ценили все выдающиеся уче­ные. М.В. Ломоносов видел в гипотезе главный путь, на котором ве­личайшие люди открывали самые важные истины. Д.И. Менделеев говорил, что гипотезы облегчают научную работу так же, как плуг земледельца облегчает выращивание полезных растений. На основе научных гипотез ведутся дальнейшие исследования закономерностей природы и общества. Научные теории, как правило, появляются на свет в виде гипотез.

Научное предположение помогает развитию производства и связан­ной с ним науки. Предвидя ход развития научного знания, гипотеза толкает вперед производство и науку. Без гипотезы не может обойтись ни одна наука.

Любая гипотеза до тех пор остается предположением, пока она не прошла стадии проверки. Естественно поэтому, что не подтвержденная гипотеза еще не является научным предположением. Чтобы выдвину­тое предположение приобрело значение научной гипотезы, его необхо­димо проверить, т.е. сравнить следствия, вытекающие из предположе­ния, с данными наблюдения и опыта.

Если в результате сравнения будет установлено, что данные наблюдения и опыта находятся в противоречии со следствиями, вытекающими из гипотезы, то в таком случае единственно правильным будет решение о том, что данная гипотеза, несомненно, ложна и должна быть отброшена. При этом гипотеза ставится под сомнение уже в том случае, когда вступает в противоречие хотя бы с одним единственным фактом. Но каждая вновь возникающая гипотеза не отбрасывает, как правило, целиком содержание прежних гипотез, а использует все рациональное, что имелось в предыдущих научных предположениях по данному вопросу.

Ценность гипотезы Лейбниц видел в ее способности объяснить возможно больше данных, установленных наблюдением, возможно меньшим числом предпосылок.

Проверенная и доказанная гипотеза переходит из разряда веро­ятных предположений в разряд достоверных истин, становится науч­ной теорией. Подобное превращение гипотезы в теорию можно пока­зать на примере научного предположения, сделанного Коперником о строении Солнечной системы. Его теория строения Солнечной систе­мы в течение трехсот лет оставалась гипотезой. Когда же астроном Леверрье на основании данных этой системы доказал, что должна су­ществовать еще одна, неизвестная до тех пор планета, и определил посредством вычисления место, занимаемое ею в небесном простран­стве, и когда в 1846 г. Галле действительно нашел эту планету (на­званную Нептуном), тогда система Коперника была доказана.

Гипотезы бывают общими и частными. Частная гипотеза — вид гипотезы, когда предположение высказывается относительно отдель­ного, частного факта, явления, в отличие от научной гипотезы, даю­щей объяснение относительно закона, присущего целому классу пред­метов. В частной гипотезе речь идет, таким образом, о предполагае­мой причине единичного частного факта, явления. Можно с уверен­ностью сказать, что с каждой моделью, как правило, связывается та или иная гипотеза или аналогия.

Создание моделей невозможно без того, чтобы не был применен метод мышления по аналогии. Конструируя модели, необходимо все время не упускать из виду, что как бы хороша ни была модель, она лишь приближенно отображает исследуемый объект, огрубляет и уп­рощает его. Если ученому удалось в модели повторить истинную структуру объекта — это свидетельство величайшего научного про­зрения. Такие случаи крайне редки, но все же встречаются. Американ­ский (а прежде отечественный) лингвист С.К. Шаумян разработал много лет назад аппликативную синтаксическую модель языка, струк­тура зависимостей элементов которой оказалась очень близкой к структуре одного из участков головного мозга, явившегося предме­том нейрофизиологического исследования научной лаборатории в США. Совпадение обнаружилось спустя много лет почти случайно и произвело настоящую сенсацию в научном мире.

Модель и оригинал очень редко оказываются сходными (тем более тождественными), ведь от модели требуется не повторение структуры объекта, а имитация его функционирования. В первую очередь отсут­ствие сходства с оригиналом, видимо, проявится в моделях мыслитель­ной формы. Но аналогия полезна уже тем, что наводит на догадки, а в этом — одна из целей моделирования.

Общим для всех выводов по аналогии является то, что непосредственному исследованию подвергается один предмет, а вывод делается о другом. Поэтому вывод по аналогии в самом общем смысле слова определяется как перенос информации с одного предмета на другой. Как уже было сказано, предмет, который является непосредственным объектом исследования, называется моделью, а предмет, на который переносится информация, добытая в результате изучения модели, на­зывается образцом, оригиналом, прототипом; аналогия — это вывод от модели к оригиналу.

Из этого видно, что моделирование — широкое понятие, которое включает в себя выводы по аналогии как неотъемлемую часть. Ана­логия в интерпретации традиционной логики имеет в виду соотноше­ние между уже данной тем или иным способом моделью и оригиналом, причем результат исследования модели в этом случае предполагается известным. В понятие же метода моделирования включается также сам процесс построения модели или нахождения ее в природе. Важным эта­пом применения метода моделирования считается исследование пост­роенной модели, получение с ее помощью необходимой информации и, наконец, практическое использование в функциях объектов моде­ли и оригинала. Но для более глубокого понимания метода модели­рования важно знание всех различных типов выводов по аналогии, известных формальной логике.

Аналогия и другие формы умозаключения — индукция и дедук­ция — неразрывно входят в единый мыслительный процесс. Они вза­имосвязаны и не могут существовать без непрерывного взаимного дополнения и взаимодействия.

Аналогия имеет определенную познавательную ценность. В про­цессе такого умозаключения получается вероятное знание, но оно не­сет в себе нечто новое, помогающее разбираться в окружающей об­становке и предвидеть направление развития данного явления или события.

Различается несколько видов аналогии.

Безусловная аналогия — аналогия, которая применяется тогда, когда точно и определенно установлена связь между общими признаками, имеющимися у обоих сопоставляемых предметов, и тем признаком, который присваивается исследуемому предмету по анало­гии с известным уже предметом. Так, в схеме умозаключения по анало­гии

А имеет признаки а + b + с;

В имеет признаки а + b + х;

Вероятно, x = c

общими будут признаки а и b, а признаком, который присваивается по аналогии исследуемому предмету, — с. Например, исследуемые млекопитающие животные имеют теплую кровь. Отношение между организацией млекопитающих и теплой кровью настолько известно, что можно сказать: теплота крови есть следствие организации животно­го. Если же затем у кита замечено несколько признаков, указываю­щих, что он принадлежит к классу млекопитающих, — то по безус­ловной аналогии можно заключить, что его кровь теплая.

Условная аналогия — такая аналогия, когда определенно не установлена связь между общими признаками, имеющимися у обо­их сопоставляемых предметов, и тем признаком, который присваива­ется исследуемому предмету по аналогии с известным уже предметом.

Простая аналогия — аналогия, в которой по сходству двух предметов в одних каких-либо признаках заключают о сходстве этих предметов в других признаках. Так, заметив, что предмет А в некото­рых свойствах сходен с другим предметом, заключают, что он сходен и в остальных свойствах.

Основанием для такого вывода служит предположение, что не случайно предметы, явления сходны в некоторых своих признаках, а потому, что они принадлежат к одному роду или виду и, следовательно, имея некоторые их черты, имеют и остальные.

Этот прием аналогии имеет значение при подведении предметов под известный род или вид, т.е. при классификации; зоолог, замечая по некоторым признакам сходство данного животного с известными ему представителями рода или вида, относит его к последним, предполагая, что в этом животном есть все, еще и не исследованные, родовые или видо­вые признаки.

Строгая аналогия — аналогия, основанная на знании того, что признаки сравниваемых предметов находятся в зависимости. Ход умозаключения идет от сходства двух предметов в одном признаке к сходству их в другом признаке, который зависит от первого. Например, студент А довольно часто строит выводы на основе поспешных обобщений, и потому рассуждения его часто бывают ошибочными. Зная, что студент Б также довольно часто делает поспешные обобщения, можно заключить, что и его рассуждения часто завершаются ошибочными выводами. В данном случае аналогия строгая, так как мы делаем заклю­чение от сходства двух лиц в одном признаке (поспешное обобщение) к сходству их в другом признаке (ошибочные выводы), который зависит от первого (ошибочные выводы есть результат поспешного обобщения).

Нестрогая аналогия — аналогия, в результате которой де­лается заключение из сходства двух предметов в известных признаках к сходству их в таком новом признаке, о котором неизвестно, на­ходится ли он в зависимости от первых или нет. Например, нам изве­стно, что медь ковка, электропроводна и теплопроводна. Изучая бе­риллий, мы установили, что он ковок и электропроводен. На основа­нии этого мы можем предположить, что бериллий также теплопрово­ден. В отличие от строгой аналогии, предполагаемый у бериллия при­знак не находится в прямой зависимости от первых известных при­знаков (ковкости и электропроводности).

Неполная аналогия — такая аналогия, когда ход умозак­лючения идет следующим образом: предметы, сходные с С по некото­рым, точно не определенным свойствам, должны производить явление В, но из известных нам знаний о предмете (или предметах) А, вслед­ствие наибольшего сходства их с С, мы имеем наибольшее основание предполагать, что он (или они) подойдет под очерченную группу, сле­довательно, имеем и больше права ожидать встретить в нем (или в них) явление В.

Значение неполной аналогии в том, что данный вывод указыва­ет путь наблюдателю или экспериментатору при исследовании явле­ния, подмеченного в известном предмете. Даже если заключение этого вывода невозможно пока проверить экспериментально, то и тогда он остается правдоподобной догадкой, которая побуждает доискивать­ся каких-либо косвенных подтверждений или опровержений ее, т.е. является исходным пунктом для новых исследований и соображений, всегда плодотворных для знания. В качестве такой догадки можно привести мысль о существовании растительной жизни на Марсе на основании значительного сходства этой планеты с Землей, которая обладает условиями для такой жизни.

Вывод по неполной аналогии — вывод от группы к частному предмету, но от группы, которая характеризуется не отвлеченными представлениями, а указанием на экземпляр, поэтому меньшая посылка может быть лишь проблематической.

Но как бы ни было значительно найденное нами сходство при­знаков двух вещей, выводы в умозаключениях по аналогии всегда бывают только вероятны. Выводы по аналогии использовать можно и нужно, но они не должны являться единственным источником наше­го знания о мире. При этом данные любой, самой верной аналогии должны проверяться на практике.

При оценке степени вероятности умозаключения по аналогии надо принимать в расчет ряд следующих условий:

1) чем больше известно общих свойств (Р ₁ ,..., P_n) у сравниваемых предметов, тем выше степень вероятности вывода по аналогии;

2) чем существеннее найденные общие свойства у сравниваемых предметов, тем выше и степень вероятности;

3) чем глубже познана взаимная закономерная связь сходных черт, тем вероятнее вывод, тем он ближе к достоверности;

4) если предмет, в отношении которого мы делаем умозаключение по аналогии, обладает каким-нибудь свойством, не совместимым с тем свойством, о существовании которого мы делаем заключение, то общее сходство не имеет никакого значения.

Данный перечень может быть дополнен такими правилами:

общие свойства должны быть любыми свойствами сравниваемых предметов, т.е. подбираться "без предубеждения" против свойств ка­кого-либо типа;

свойство Р_{n +1}, т.е. свойство, обнаруженное в модели, должно быть того же типа, что и общие свойства (Р ₁ ,..., P_n);

общие свойства (Р ₁ ,..., P_n) должны быть возможно более специфичными для сравниваемых предметов, т.е. принадлежать возможно меньшему кругу предметов;

свойство Р_{n +1} наоборот, должно быть наименее специфичным, т.е. принадлежать возможно большему кругу предметов.

При употреблении аналогии, предупреждал русский логик Л. Рутковский, нужна большая осторожность. "Лучшее средство против погрешностей аналогического умозаключения состоит в проверке основания, на котором оно утверждается. Поэтому нужно наблюдать, существенны ли и в каком количестве представляются сходные призна­ки между предметами, которые мы сближаем посредством аналогичес­кого умозаключения. Чем в большем числе существенных признаков сходны сравниваемые предметы, тем вероятнее их одинаковость и в других отношениях; чем короче мы знакомы с особенным устройством этих предметов, тем выводы наши по аналогии бывают основатель­нее и более приближаются к истине".

В одной из своих ранних работ Ломоносов писал, что "уподобле­ния не доказывают, а лишь объясняют доказанное".

Каков главный недостаток и какое главное достоинство доказа­тельства по аналогии? Главный недостаток заключается в том, что, как уже подчеркивалось, такое доказательство нестрогое, оно носит гипо­тетический характер. А самое главное достоинство этого доказатель­ства: его с большой легкостью и естественностью воспринимают слу­шатели. Почему? Потому что восприятие мира по аналогии есть гене­тическое, врожденное свойство каждого человека. С самого раннего дет­ства мы познаем мир по аналогии с нашим собственным опытом и опы­том людей, которые жили больше, чем мы, в частности с опытом родителей. Как человек понимает, что трогать кипящий чайник не надо? Во-первых, потому что ему об этом сказали мама с папой и, во-вторых, по­тому что однажды, схватившись, он обжегся. Мы не трогаем чайник по аналогии с теми ощущениями, которые у нас уже были или которым нас научили. Почему мы надеваем зимой шубу? Потому что наш личный опыт показывает, что если выйти в куртке, то холодно, а если выйти в шубе, то комфортно. Эти примеры можно продолжать бесконечно, так как огромное количество поступков, которые мы совершаем, суть поступ­ки, совершенные по аналогии. Аналогия естественна для человеческой природы, человеческого интеллекта. Поэтому, апеллируя к этой особен­ности человеческого интеллекта, мы находим очень внимательного и удовлетворенного нашими доводами слушателя. Представьте себе ситу­ацию, когда вам надо попросить субсидию для производства кинокар­тины. Вы приходите к спонсору и говорите: "Эту картину я хочу зака­зать режиссеру X, который снял на сегодняшний день четыре фильма. Посмотрите: фильм первый дал в прокате два миллиона долларов при­были, фильм второй дал в прокате полтора миллиона долларов, фильм третий был несколько менее коммерческим, но, тем не менее, окупился с прибылью в полмиллиона долларов, ну а четвертый фильм — просто бе­стселлер, мировая сенсация, окупил себя пять раз и до сих пор не снят с проката". Убедительное доказательство? Убедительное. Если из четырех снятых фильмов все были коммерчески очень выгодны, есть немалая ве­роятность того, что деньги, вложенные в пятый фильм, принесут прибыль. Индуктивное доказательство кажется порой излишне скрупулезным, де­дуктивное доказательство — слишком догматичным. А доказательство по аналогии настолько для человека естественно, что он даже подчас не осознает, что ему что-то доказывают.

В умозаключениях по аналогии возникают ошибки. Главный ис­точник заблуждения состоит в том, что умозаключающий может не об­ратить внимания на те свойства сравниваемых предметов, которыми они отличаются друг от друга. В таких случаях аналогия ведет к оши­бочным заключениям.

Ложная аналогия возникает и в тех случаях, когда общие признаки не связаны с тем, который является предметом доказательства. Рассмот­рим пример. Представим себе, что в формуле 1 (см. начало главы) под A понимается не горный массив Калифорнии, а медведь, которого зовут Мишка, а под В понимается другой медведь, которого зовут Гришка. Эти медведи оказались обладающими большим количеством одина­ковых признаков: первый медведь — самец и второй — самец (при­знак a ₁). Первый медведь — крупный, второй — тоже крупный (а ₂ ), первый медведь агрессивный и второй — агрессивный (а ₃ ), первый медведь — физически здоровый и второй — физически здоровый (a_n).

У первого медведя есть дополнительный признак а_{n+ 1}: он бурый. Можно ли с уверенностью утверждать, что второй медведь — Гришка — тоже бурый? Нет. Почему же в ситуации с золотом сделать утверждение по аналогии можно, а в ситуации с медведем — нельзя? Схема ведь та же самая. Чего не хватает, почему не получается доказательство? Почему если есть олово, цинк, свинец, железная руда, естественно предположить наличие золота? А почему пол, размер, агрессивность и состояние здо­ровья не дают основания предполагать, что второй медведь тоже бу­рый? Если у них общие родители, т.е. они братья, — тогда можно пред­положить, что они оба бурые, если бурый первый. Если ввести в набор единообразных признаков общих родителей или такой признак, как среда обитания, то тогда из того, что первый бурый, будет очевидно следовать, что и второй бурый. Это означает, что признаки a₁ — а_{n+ 1} должны быть связаны между собой. Цвет и пол — не связанные друг с другом признаки, размер и окрас — не связанные друг с другом при­знаки, и т.д. Реально все признаки, которые были перечислены для этих двух медведей, не связаны с признаком окраса. А вот среда обитания или наличие общих родителей связаны с признаком окраса, и поэтому введение данных признаков делает доказательство адекватным.

Развитие научной мысли знает много примеров ложной анало­гии. Результатом ошибочной аналогии было мнение древних астро­номов о том, будто темные плоские пространства на поверхности Луны представляют моря. Они рассуждали так: Луна подобно Земле долж­на иметь моря и океаны. Когда же с помощью мощных телескопов было установлено, что темные места на Луне — это длинные тени от гор, то прежняя аналогия была отброшена как неверная.

Каждый педагог по своему опыту знает, что значительное количе­ство логических ошибок, допускаемых учащимися, есть результат не­верных умозаключений по аналогии. Так, наличие некоторых сходных свойств в действиях сложения и умножения известно с первых классов начальной школы. И сложение, и умножение подчиняются переместительному и сочетательному законам. Зная это, ученики иногда при­ходят к ошибочной аналогии, что арифметические действия сходны и в остальных свойствах.

Ошибочная аналогия нередко приводит к печальным результатам. Так, дети иногда собирают и едят ядовитые ягоды, ошибочно заклю­чая, что их можно есть, потому что другие ягоды, несколько сходные с ними по внешнему виду, оказывались вкусными.

Таким образом, доказательство по аналогии получается только в том случае, когда общие признаки объектов и искомый признак (т.е. тот, который ищется в доказательстве) оказываются связанными меж­ду собой.

Наибольшее значение аналогия имеет при изучении и объяснении связи причин и действий. Укажем два случая. Во-первых, когда от сходных явлений приходится делать заключение о сходстве произвед­ших их причин. Во-вторых, когда от сходных причин приходится де­лать заключение о сходстве производимых ими действий. Такая ана­логия называется распространенной.

То есть любые случаи распространенной аналогии могут быть разделены на те, которые относятся к прошлому, и те, которые относят­ся к будущему. Аналогия, устремленная в прошлое, это попытка воссоздать причину по имеющемуся результату. Модель такова: известно, что некоторое следствие В обычно является производной от некоторой причины А; возникает феномен В, который человек наблюдает и вос­станавливает причину этого феномена в виде А. Если наблюдаются при­знаки, причина порождения которых известна, восстанавливается сама причина. На принципе аналогии, устремленной в прошлое, построена медицинская диагностика. Как ведет себя доктор? Он наблюдает симп­томы: жалобы пациента, результаты анализов и др. Доктора когда-то учили, что симптоматика такого рода есть следствие некоторого заболе­вания К. Кроме того, его медицинский профессиональный опыт дает ему основание предполагать, что его учили правильно. Действительно, каж­дый раз эти симптомы оказывались следствием заболевания К. Наблю­дая вновь ту же симптоматику, доктор делает заключение, что его паци­ент болен заболеванием К. К сожалению, достаточно часто диагноз ока­зывается неверным, т.е. причина восстанавливается неправильно. По­чему ставятся неверные диагнозы? Разве был неудачный жизненный опыт? Нет. Просто человек и его организм так сложно устроены, что одна и та же симптоматика может быть результатом разных заболеваний. На­пример, если человек физически слабый, т.е. у него ослаблен весь орга­низм, в частности нервная система, достаточно серьезные симптомы мо­гут быть следствием и незначительного заболевания. Если же человек крепкий и выносливый, то даже тяжелое заболевание может не давать очень сильной симптоматики. Каковы погрешности в точности диагно­за, т.е. погрешности, связанные с аргументацией по аналогии? Диаг­ноз может оказаться неверным в определении стадии заболевания, тогда аналогия оказывается неверной частично. Но диагноз может быть не­верным полностью. Например, болезненное состояние организма может быть связано с разрывом энергетического поля, ауры вокруг тела чело­века, которая нас защищает и в которой иногда возникает брешь. В эту брешь попадает пучок отрицательной энергии, пагубно влияя на тот орган, около которого брешь пробита. Орган не болен, а просто пучок отрицательной энергии давит на него. Это феномен, о котором сейчас много говорят. Таким образом, первая причина неверного диагноза: сим­птоматика определена не тем, что это больной орган, а тем, что это "не­везучий" орган, который оказался первым на пути пучка отрицатель­ной энергии, проникшей в организм, и "принял удар на себя". Возмож­на и другая причина: заболевание может быть связано не с тем органом, который болит. Заболевание есть, но оно локализовано в другом месте. Например, в мозге человека. Очень часто симптоматика болезни любого органа есть на самом деле симптоматика болезни психической. Приве­дем достоверный пример, который заставляет задуматься не столько о чудесах медицины и диагностики, сколько вообще об относительности интерпретации того, что мы наблюдаем.

Одна девушка много лет страдала заболеванием печени: у нее часто бывали приступы, наблюдалась сильная боль в пра­вом боку, озноб и другие симптомы. У нее были очень обеспеченные родители (папа был известным адвокатом), которые не жалели ни сил, ни средств для лечения дочери, бывали и в Трускавце, и в Карловых Варах, и в Пятигорске. Каких только вод эта девушка не пила, и у каких только врачей она не лечилась. Был даже доктор из Швейцарии. От многолетнего лечения ре­зультат был скорее отрицательный, поскольку с каждым годом ей становилось все хуже и хуже. Ей ставили диагноз: холецис­тит и засорение желчных протоков. Однажды в доме адвоката и его дочери случайно оказался врач-психиатр: он нанял адвоката — отца этой девушки — для ведения личного дела. Они сидели в гостиной и обсуждали правовые проблемы, а в это время дочка, которая тоже находилась в гостиной, почувство­вала себя плохо, потом все хуже и хуже — у нее начался при­ступ. Отец очень разволновался, бросился за лекарствами и ре­шил вызвать "Скорую помощь". В этот момент психиатр, ко­торый наблюдал, как развивается приступ, сказал адвокату: "Я же все-таки врач, не надо "Скорой помощи". Я попробую ей сам снять приступ". На что адвокат возразил: "Но вы же не гастроэнтеролог!" "Ничего, — ответил доктор, — я врач, я попро­бую, только вы мне не мешайте, выйдите из гостиной, пожалуй­ста, ненадолго". Отец вышел. Психиатр поговорил с девушкой в течение нескольких минут, и приступ у нее стал утихать и вскоре прошел. Растерявшийся от неожиданности и радости отец не знал, как отблагодарить врача, но психиатр его очень расстро­ил, сказав, что девушка, конечно, больна, но печень у нее совер­шенно здорова, зато у нее шизофрения. "Если вы хотите, чтобы у нее перестала болеть печень, ее следует положить ко мне в клинику", — сказал психиатр. И действительно, девушку положили в психиатрическую больницу, долго лечили психотропными сред­ствами — печень у нее уже 20 лет не болит. Что же произошло? На протяжении многих лет ее диагностировали лучшие гастроэнтерологи, находили у нее заболевания, подтвержденные ана­лизами и рентгеноскопией, которых просто не было. У нее оказа­лись так называемые фантомные боли и фантомные симптомы. Ей действительно казалось, что у нее болит печень, что ее тошнит и знобит, а на самом деле ничего этого с ней не происходило, а был страх перед болью и внутренняя уверенность в том, что от этой боли нет исхода, что является симптомом тяжелого психи­ческого заболевания, которое, к счастью, удалось вылечить. Этот пример доказывает относительность медицинской диагнос­тики, построенной на принципе аналогии.

Не нашли, что искали? Воспользуйтесь поиском: