Нахождение корней уравнения

Метод простых итераций

Исходное нелинейное уравнение записываем в виде x = f(x). Подставляем начальное значение корня x = c₀ в правую часть уравнения, получаем новое приближение с₁ = f(c₀) и т.д. Получаем с_n+1 = f(c_n), n=0,1,2, … Итерационный процесс прекращается, если результаты двух последних итераций близки, т.е. ½ c_n+1 - c_n ½ < e. Предусмотреть защиту от зацикливания.

Метод деления отрезка пополам

Пусть на отрезке [ a,b ] существует корень уравнения, и на [ a, b ] функция меняет знак. В качестве начального приближения корня принимают середину отрезка [ a, b ], т.е. c₀= . Исследуют функцию f(x) на концах отрезков [ a, c₀ ] и [ с₀, b ]. Тот из них, на концах которого f(x) принимает значения разных знаков, содержит корень. Его принимаем в качестве нового отрезка [ a, b ]. Находят середину вновь полученного отрезка и т.д. Итерационный процесс продолжаем до тех пор, пока значение функции f(x) после n- ой итерации не станет по модулю меньше допустимой погрешности e, т.е. | f(x) | < e, или если длина интервала становится меньше заданной точности, т.е.
| b - a| < e.

Метод хорд

На отрезке [ a, b ] функция f(x) меняет знак. В качестве приближений к корню принимают точки с₀, с₁, с₂, … пересечения хорды с осью абсцисс, т.е. на первом шаге с₀ = a - ,если f(b) > f(a)
с₀ = b - , если f(b) < f(a).

Получаем отрезки [ a, с₀ ] и [ с₀, b ]. Тот отрезок, на концах которого f(x) принимает значения разных знаков, содержит искомый корень. Его принимают в качестве нового отрезка. Находим на вновь полученном отрезке точку пересечения хорды с осью абсцисс по формулам, изложенным выше и т.д. Итерационный процесс продолжаем до тех пор, пока значение функции f(x) после n‑ой итерации не станет меньшим по модулю некоторой заданной точности e, т.е. | f(x) | < e, или если длина интервала становится меньше заданной точности, т.е. | b - a| < e.

1. Найти с точностью 0,001 корень уравнения x² cos 2x + 1 = 0 на отрезке методом простых итераций.

2. Определить корень уравнения c точностью e =10^-5 на отрезке [-1; 2] методом простых итераций.

3. На отрезке [-2; 1] найти корень уравнения x³ + x² + x + 1 = 0 методом простых итераций.

4. На отрезке [0; 1] найти корни уравнения x⁵ - 0,3½x-1½=0 методом простых итераций.

5. На отрезке найти корни уравнения 2x - cos x = 0 методом простых итераций.

6. На отрезке [0; 1,5] найти корни уравнения 0,9x - sin - 0,1 = 0 методом простых итераций.

7. На отрезке 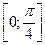найти корни уравнения tg x = 0 методом простых итераций.

8. Составить программу решения уравнения sin x² + cos x²-10x = 0 методом деления отрезка пополам. Известно, что значение корня находится на отрезке [0; 1].

9. Методом деления отрезка пополам найти корень уравнения x³ + 3x - 1 = 0 на отрезке [-2; 1].

10. Методом деления отрезка пополам найти корень уравнения 2^x + 5x - 3 = 0 на отрезке [0; 10].

11. Методом деления отрезка пополам найти корень уравнения x⁴ - x - 1 = 0 на отрезке [0; 3].

12. Методом хорд найти корень уравнения sin 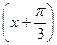- 0,5x = 0 на отрезке .

13. Методом деления отрезка пополам найти корни уравнения log ₂ (-x)(x+2) = -1 на отрезке [-8; -1].

14. Методом хорд найти корень уравнения arctg x + = 0 на отрезке .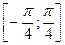

15. Методом деления отрезка пополам найти корень уравнения (x-3)cos x - 1 = 0 на отрезке .

16. Методом хорд найти корень уравнения 0,5^x + 1 = (x²-2)² на отрезке [-2; 5].

17. Методом деления отрезка пополам найти корень уравнения x-cos x = 0 на отрезке .

18. Методом деления отрезка пополам найти корень уравнения 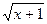= на отрезке [0,1; 10].

19. Методом хорд найти корень уравнения 5^x - 8x³ = 0 на отрезке [-2; 2].

20. Методом хорд найти корень уравнения x 2^x = 1 на отрезке [-2; 5].

21. Методом хорд найти решение уравнения x⁴ - 2 = 0 на отрезке [0; 3].

22. Методом хорд найти корень уравнения x³ + x - 2 = 0 на отрезке [0; 2].

23. Методом деления отрезка пополам найти корень уравнения cos x- + x - 1 = 0 на отрезке [1; 2].

24. Методом хорд найти корень уравнения x - 2 + sin = 0 на интервале [1,2;2].

25. Методом хорд найти корень уравнения x³-x²+2=0 на отрезке [-2; 0].

26. Методом деления отрезка пополам найти корень уравнения x³ - 6x + 2 = 0 на отрезке [-3; 3].

27. Методом деления отрезка пополам найти корень уравнения tg x - 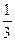tg³ x+ tg⁵x - 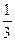=0 на отрезке [0,1; 0,8].

28. Методом хорд найти корень уравнения e^x+ ln x-10x=0 в интервале [3; 4].

29. Методом хорд найти корень уравнения x³-1=0 на отрезке [-1; 2].

30. Составить программу решения уравнения методом простых итераций x - = 0. Для отладки программы взять х₀ = 0,5.

Задания

Не нашли, что искали? Воспользуйтесь поиском: