Лабораторная работа 7

Массивы

Цель работы – изучение основных понятий и принципов организации и использования массивов, получение навыков составления программ с индексированными переменными. В практике расчётов часто приходится иметь дело с совокупностью однородной информации. Например, зарплата работников какого-то подразделения имеет разные значения, но очевидно, нет смысла использовать разные переменные.

Для обозначения одинаковых по смыслу, но различных значений переменных в программировании используют так называемые индексированные переменные, или переменные с индексами, которые объединяются в массивы. Массив – совокупность индексированных переменных, имеющих одно имя, но отличающиеся друг от друга порядковыми номерами (индексами) и своими значениями.

По способу организации различают одномерные массивы – векторы и двумерные – матрицы. Примером одномерного массива является n-мерный вектор: x_1, x_{2, ….,} x_n. Матрица в общем виде записывается следующим образом:

a₁₁a₁₂a₁₃ … a_1n

a₂₁a₂₂a₂₃ … a_2n

_.

_.

_.

a_m1a_m2a_m3 … a_mn

Правила работы с массивами:

1. все используемые в программе массивы должны быть объявлены;

2. ввод, вывод, обработка массивов осуществляется в цикле;

3. значения индексов не должны выходить за указанные в объявлении массива пределы;

4. для обращения к элементу массива нужно определить его индекс.

Задания

Одномерные массивы

1. Дан вектор А(а₁,а₂,...,а₁₀₀).Упорядочить компоненты вектора так, чтобы сначала размещались все отрицательные компоненты, затем все положительные, а потом нулевые.

2. Ввести массив А(а₁,а₂,...,а₁₀). Подсчитать количество положительных и отрицательных элементов массива.

3. Ввести массив А(а₁,а₂,...,а₁₀). Подсчитать количество всех чисел, расположенных в промежутке [-1;1], и сумму всех остальных.

4. Даны массивы X(x₁,x₂,...,x₁₀) и H(h₁,h₂,...,h₁₀). Сформируйте новый массив Y(y₁,y₂,...,y₁₀) по следующему правилу:

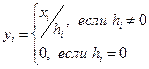
5. Даны массивы X(x₁,x₂,...,x₁₀) и H(h₁,h₂,...,h₁₀). Найдите
, где n =10

6. Дан массив X(x₁,x₂,...,x₁₀). Найдите
,где , n =10.

7. Дан массив X(x₁,x₂,...,x₁₀). Найдите
,где

8. Дан массив X(x₁,x₂,...,x₁₀). Распечатайте отрицательные элементы массива и найдите сумму положительных элементов.

9. Даны числа x, y и массив A(a₁,a₂,...,a₁₀). Образуйте массив B(b₁,b₂,...,b₁₀) по правилу:

10. Даны массивы X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀). Вычислите сумму
, где n =10. Подсчитайте число нулевых элементов.

11. Дан массив X(x₁,x₂,...,x₁₀). Найдите произведение всех положительных и сумму всех отрицательных элементов.

12. Дан массив А(а₁,а₂,...,а₁₀). Все элементы, стоящие после максимального, заменить нулями.

13. Дан массив X(x₁,x₂,...,x₁₀). Образовать массив Y(y₁,y₂,...,y₅), элементы которого определяются как

14. Даны массивы X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀). Образовать массив Z, элементы которого определяются следующим образом:

15. Вычислить математическое ожидание М и дисперсию D по формулам:
,
, где (а₁,а₂,...,а₁₀) задать вводом.

16. Дан массив X(x₁,x₂,...,x₁₀). Создать новый массив Y(y₁,y₂,...,y₁₀), элементы которого вычисляются следующим образом:

17. Найти среднее арифметическое элементов А(а₁,а₂,...,а₁₀), предшествующих первому отрицательному элементу

18. Даны массивы X(x₁,x₂,...,x₁₀)и Y(y₁,y₂,...,y₁₀). Сформировать новый массив Н(h₁,h₂,...,h₁₀) по правилу:

19. Ввести массив X(x₁,x₂,...,x₁₀). Подсчитать количество элементов, чье значение больше 1, а также найти сумму отрицательных элементов.

20. Даны массивы X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀). На место массива Х записать массив Y, а на место массива Y – массив Х.

21. Даны массивы X(x₁,x₂,...,x₁₀)и Y(y₁,y₂,...,y₁₀). Сформировать массив Z(z₁,z₂,...,z₂₀) по правилу:

22. В массиве А(а₁,а₂,...,а₁₀) вычислить сумму отрицательных, произведение положительных и количество нулевых элементов.

23. Найти среднее арифметическое значение элементов массива X(x₁,x₂,...,x₁₀), предшествующих первому положительному элементу.

24. Дан вектор А(а₁,а₂,...,а₁₀). Упорядочить элементы вектора так, чтобы сначала размещались всё отрицательные элементы, а затем все положительные.

25. Даны два вектора X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀).Найти значение

26. Даны два вектора X(x₁,x₂,...,x₁₀) и P(p₁,p₂,...,p₁₀). Найдите
, где n =10.

27. Дан вектор А(а₁,а₂,...,а₁₀). Найти длину вектора по формуле

28. Для вектора исходных данных Х вычислить оценку эксцесса:
, где , , n – количество элементов вектора Х.

29. Для вектора исходных данных Х вычислить оценку асимметрии:
, где , , n – количество элементов вектора Х.

30. Даны целые а₁,а₂,...,а₂₀. получить суммы тех чисел , которые
1) кратны 5;
2) нечетные;
3) отрицательны.

Задания

Двумерные массивы

1. Введите 10 координат Х(х₁, х₂,..., х₁₀) и 10 координат Y(y₁, y₂,..., y₁₀). Сгенерируйте матрицу М(х_i, y_i). Подсчитайте число точек М(х_i, y), которые попали в заданную область.

2. Даны матрицы А(3,3) и В(3,3). Сформируйте матрицу С(3,3) по следующему правилу:

Выведите на печать все три матрицы.

3. Дана матрица А(5,5). Построить вектор В(b₁,..., b₅) по следующему правилу:
b_i – число ненулевых элементов в i-той строке. Выведите на печать матрицу А и вектор В.

4. Даны матрицы А(3,3) и В(3,3). Сформировать матрицу С(3,3) по правилу:

Выведите на печать все три матрицы.

5. Дана матрица А(3,5). Сформировать вектор В(b₁,..., b₅) по правилу:

Выведите на печать матрицу А и вектор В.

6. Даны матрицы А(5,6) и В(6,3). Сформировать матрицу С(5,3), равной произведению матриц А и В. Выведите на печать матрицу С.

7. Дана матрица А(5,5). Найдите среднее арифметическое элементов, расположенных под главной диагональю; на главной диагонали; над главной диагональю. Напечатайте матрицу А и значения средних арифметических.

8. Дана матрица А(4,5) и вектор В(b₁,..., b₆). Сформировать матрицу С(4,5), каждый элемент которой вычисляется по формуле , где - максимальный элемент вектора В. Напечатать матрицу С.

9. Даны два вектора Х(х₁,..., х₅) и Y(y₁,..., y₅). Сформировать матрицу А(5,5) и вывести ее на печать. ,где i =1,2,...,5 j =1,2,…,5

10. Дана матрица В(5,6). На место последнего элемента каждого столбца записать произведение предшествующих ему элементов в этом столбце. Распечатать вновь полученную матрицу В.

11. В матрице А(5,6) найти среднее арифметическое всех элементов, удовлетворяющих условию: . Вывести на печать матрицу А и среднее арифметическое значение.

12. Преобразовать исходную матрицу А_nxm следующим образом: поэлементно вычесть последнюю строку из всех строк, кроме последней. (n=5, m=7).

13. Найдите , где n – количество нулевых элементов матрицы А(5,5). Распечатайте матрицу А и значение k.

14. В матрице А(6,6) все поддиагональные элементы замените нулями. Распечатайте вновь полученную матрицу А(6,6). Вычислить произведение элементов, стоящих выше главной диагонали, и сумму элементов, стоящих на диагонали.

15. Сформируйте матрицу А(10,10) по правилу:

Распечатайте полученную матрицу.

16. В матрице У(4,5) в каждом столбце найдите сумму элементов, лежащих в интервале 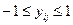. Образовать из этих сумм пятую строку исходной матрицы. Распечатать вновь полученную матрицу У(5,5).

17. Дана матрица А(4,5). Образуйте матрицу В(5,4) путем транспонирования матрицы А (строки и столбцы поменять местами). Выведите на печать матрицы А и В.

18. Дана матрица А(5,5). Вычислить сумму элементов, расположенных ниже главной диагонали. Напечатайте матрицу А и значение суммы.

19. Дана матрица А(5,6). Сформировать вектор В(b₁,..., b₅), i-тая компонента которого равна количеству нулевых элементов i-той строки матрицы А. Вывести на печать матрицу А и вектор В.

20. Дана матрица А(5,6). На место последнего элемента каждой строки записать сумму предыдущих ему элементов в этой строке. Распечатать вновь полученную матрицу А.

21. В матрице С(5,6) найти среднее арифметическое всех элементов, удовлетворяющих условию . Вывести не печать матрицу С и значение среднего арифметического.

22. В матрице А(5,6) определить max и min элементы и поменять их местами. Вывести на печать вновь полученную матрицу А.

23. В матрице А(4,5) определить среднее арифметическое положительных и отрицательных элементов. Подсчитать количество нулевых элементов. Распечатать матрицу А(4,5), значение среднего арифметического и число нулевых элементов.

24. Для каждой строки матрицы А(4,5) найти средние арифметические значения и сформировать вектор M(m₁,..., m₅). Распечатать матрицу А и вектор М.

25. В матрице D(6,4) найти сумму элементов каждой четной строки и произведение элементов каждой нечетной строки, сформировав из них вектор А(a₁,..., a₆). Вывести на печать матрицу D и вектор А.

26. В матрице Х(6,4) в каждой строке найдите сумму элементов, лежащих в интервале . Образовать из этих сумм пятый столбец исходной матрицы. Распечатать вновь полученную матрицу Х(6,5).

27. Дана матрица А(3,4). Образовать матрицу В(3,4) путем деления всех элементов матрицы А на ее максимальный элемент. Вывести на печать матрицы А и В.

28. В матрице А(5,5) найти сумму элементов, расположенных в строках с отрицательным элементом на главной диагонали. Напечатать матрицу А и значение суммы.

29. Дана матрица В(5,5). Вычислить произведение элементов, стоящих выше главной диагонали. Напечатать матрицу В и значение произведения.

30. Дана матрица А(3,3). Построить векторы В (b₁, b₂, b₃), i-тая компонента которого равна количеству положительных элементов i-той строки матрицы А; и вектор С(с₁, с₂, с₃), i-тая компонента которого равна количеству отрицательных элементов i-той строки матрицы А. Вывести на печать А, В и С.

Не нашли, что искали? Воспользуйтесь поиском: