Процедуры - функции

1. Даны матрицы А(4,4) и В(9,9). Вычислить

S_A – след матрицы А, S_B – след матрицы В (сумма элементов главной диагонали). Вычисление следа матрицы оформить процедурой-функцией.

2. Сформировать три диагональные матрицы А(5,5), В(4,4) и С(6,6). Найти наименьший определитель матриц А, В, С (определитель диагональной матрицы – произведение элементов главной диагонали). Формирование матрицы оформить в виде процедуры. Вычисление значения определителя оформить в виде процедуры-функции.

3. Даны матрицы А(2, 2), В(2, 2), С(2, 2), D(2, 2), Е(2, 2). Сформировать вектор , где - значение определителя для матриц: f₁ для А, f₂ для В, f₃ для С, f₄ для D, f₅ для Е. Найти длину вектора f. Нахождение длины вектора и значений определителей оформить процедурой-функцией.

4. Даны две матрицы А(5, 6) и В(7, 3). Вычислить , где с – произведение отрицательных элементов матрицы А, d – произведение отрицательных элементов матрицы В. Произведение отрицательных элементов матрицы оформить процедурой-функцией.

5. Даны две матрицы А(3,9) и В(6,6). Вычислить , где с и f – количество положительных элементов матриц А и В, d и е – количество отрицательных элементов в матрицах А и В соответственно. Вычисление количества положительных и отрицательных элементов оформить в виде процедур-функций.

6. Даны векторы , , , 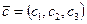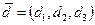. Вычислить , где х – скалярное произведение векторов 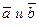, y – скалярное произведение . Скалярное произведение оформить в виде процедуры-функции.

7. Даны матрицы А(3, 3), В(4, 4) и С(5, 5). Найти наибольшее из чисел x, y, z, где x – след матрицы А, y – след матрицы В, z – след матрицы С. Вычисление следа матрицы (сумма элементов главной диагонали) оформить в виде процедуры-функции.

8. Решить уравнение ax=b, где a – длина вектора 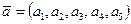, b – длина вектора . Вычисление длины вектора оформить в виде процедуры-функции. Длина вектора .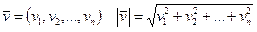

9. Ввести матрицы А(3,6) и В(7,5). Вычислить 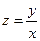, где x – максимальный элемент матрицы А, y – максимальный элемент матрицы В. Вычисление максимального элемента оформить в виде процедуры-функции.

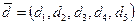10. Даны два вектора и . Вычислить 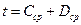, где и 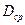- среднеарифметические значения в векторах c и d соответственно. Вычисление среднеарифметического оформить в виде процедуры-функции.

11. Даны два вектора 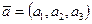и . Вычислить 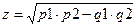, где p1, q1 – max и min соответственно в векторе А; p2, q2 – max и min соответственно в векторе В. Вычисление max и min оформить в виде процедур-функций.

12. Даны С(5, 6), Д(5, 6), А(7, 3) и В(7, 3). Просуммировать элементы матрицы В, которым соответствуют элементы матрицы А, для которых 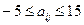. Аналогично просуммировать элементы матрицы Д, которым соответствуют элементы матрицы С, для которых . Вычисление суммы оформить в виде процедуры-функции.

13. Даны матрицы А(5, 7), В(3, 2), С(7, 11). Используя процедуру-функцию, для каждой матрицы найти количество элементов, отличных от нуля. На печать вывести среднеарифметическое среди этих трех значений.

14. Даны матрицы А(7, 9), В(5, 3), С(15, 9). С помощью процедуры-функции сформировать новые матрицы А1(7, 9), В1(5, 3), С1(15, 9), разделив элементы исходных матриц на их минимальный элемент. На печать вывести минимальные элементы в основном блоке.

15. Даны две матрицы А(5, 6) и В(10, 15). Для каждой матрицы найти минимальный элемент в каждом столбце матрицы и записать их в виде одномерных массивов С и D с помощью процедуры. С помощью процедуры-функции вычислить суммы элементов вектора С и аналогично для D.

16. Для матриц А(5, 4) и В(6, 7) сформировать векторы С(6) и D(6), где c_i – среднеарифметическое i -ой строки матрицы А, 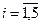, d_i – среднеарифметическое i -ой строки матрицы В, 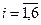. Вычисление среднеарифметического оформить в виде процедуры-функции, а формирование векторов – в виде процедуры.

17. Даны матрицы А(4,5) и В(6,7). Сформировать векторы С(5) и D(7). c_j – сумма элементов j -го столбца матрицы А, , d_j – сумма элементов j -го столбца матрицы В, 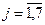. Формирование векторов оформить процедурой. Вычислить z=xy, где x – длина вектора С, y – длина вектора D. Вычисление длины вектора оформить в виде процедуры-функции.

18. Сформируйте матрицы А(7, 9) и В(9, 7) по формулам . Вычислить z=c-d, где с – произведение минимальных элементов каждого столбца матрицы А, d – произведение минимальных элементов каждого столбца матрицы В. Формирование матрицы оформить процедурой, вычисление произведения – процедурой-функцией.

19. Даны матрицы А(3,3) и В(5,5). Если след матрицы А больше следа матрицы В, то , иначе . Вычисление следа матрицы (сумма элементов главной диагонали) оформить в виде процедуры-функции.

20. Для матриц Х(5, 9) и У(17, 8) найти sum1 и sum2 соответственно – суммы элементов, не превышающих 1. Поиск сумм оформить в виде процедуры-функции. Если sum1 > sum2, то с помощью процедуры транспонировать матрицу Х, иначе – матрицу У.

21. Вычислить , , 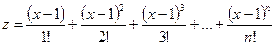, где x, n задавать вводом. Вычисление сумм оформить в виде одной и той же процедуры-функции. Найти наибольшее среди y, z, w (с помощью другой процедуры).

22. Ввести вектора 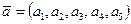, , 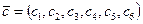. Если , то , иначе 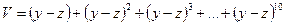, где x, y, z – длины векторов 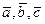соответственно. Вычисление длины вектора и значения V оформить в виде процедур-функций.

23. Даны , , 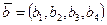. Если , то , иначе , где x, n задать вводом. Вычисления y и скалярного произведения оформить в виде процедур-функций, вычисление сумм с помощью другой процедуры-функции. , k – количество элементов в векторе.

24. Даны две матрицы А(5, 7) и В(6, 6). Вычислить z=cd, где с – произведение элементов, стоящих в четном столбце матрицы А, d – произведение элементов, стоящих в четном столбце матрицы В. Нахождение произведения элементов в четном столбце оформить в виде процедуры-функции.

25. Найти минимальное значение среди 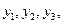где
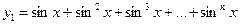, , , где вычисление суммы оформить в виде одной (!) процедуры-функции. Значения x, n задать вводом.

26. Даны матрицы А(5, 4) и В(4, 5). Вычислить след матрицы . Вычисление следа матрицы оформить в виде процедуры-функции. След – сумма элементов главной диагонали.

27. Для матрицы А(5, 6) найти минимальное значение суммы элементов каждой строки. Вычисление суммы оформить в виде процедуры-функции. Аналогично для матрицы В(8, 3).

28. Даны две матрицы А(5, 4) и В(6, 3). Найти максимальное значение из сумм элементов каждого столбца. Вычисление сумм элементов столбца оформить в виде процедуры-функции.

29. Вычислить углы между прямыми 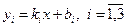. Вычисление угла оформить в виде процедуры-функции. С помощью процедуры вывести на печать максимальный и минимальный угол.

30. Вычислить углы между прямыми: 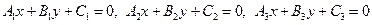. Вычисление угла оформить в виде процедуры-функции. Вывести на печать максимальный и минимальный угол. Поиск максимального и минимального углов оформить процедурой.

Не нашли, что искали? Воспользуйтесь поиском: