Доказательство (см. [2]).

Сначала отметим, что из условий теоремы сразу следует асимптотическая устойчивость по Ляпунову при тривиального решения согласно второй теореме Ляпунова об асимптотической устойчивости (см. п. 2.1).

Докажем экспоненциальную устойчивость тривиального решения системы.

Из теоремы о свойствах вещественных квадратичных форм (см. выражение (1.5.7 из п. 1.5.2) следуют следующие двухсторонние оценки - неравенства:

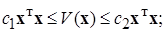(2.3.12) 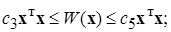(2.3.13)

где положительные числа , и , - минимальные и максимальные собственные значения матриц В и С соответственно:

(2.3.14)

причем - евклидова норма вектора ,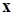

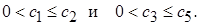
Отсюда на основании неравенств (2.3.10) и (2.3.13) получим, усиливая неравенство (2.3.10) (подставляя в него - :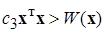

(2.3.15)

Используя (2.3.12), усилим полученное неравенство (2.3.15) (подставляя 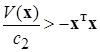) так:

(2.3.15’)

Полученное неравенство (2.3.15) и (2.3.15’) для полной производной функции Ляпунова, вычисленной в силу приведенной системы, является решающим для установления факта экспоненциальной устойчивости ее тривиального решения. Действительно, проинтегрируем неравенство (2.3.15’) на полубесконечном интервале 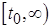. Будем иметь:

(2.3.16)

где обозначено

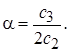
Далее, используя оценку евклидовой нормы из (2.3.12) при 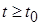, находим

.

Используя неравенства (2.3.16) и (2.3.12), усилим последнее неравенство:

Извлекая из обеих частей последнего неравенства квадратные корни, получим:

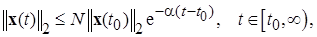(2.3.17)

где

(2.3.18)

Неравенство (2.3.17) в точности совпадает с определением экспоненциальной устойчивости для случая нулевого фиксированного решения (см. п.1.2, определение 4).

Таким образом, доказано, что тривиальное решение приведенной системы (2.1.1)÷(2.1.3) при выполнении условий теоремы будет экспоненциально устойчиво с постоянными N и , вычисляемыми по формулам (2.3.18) и (2.3.14) и областью экспоненциального притяжения

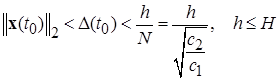, (2.3.19)

где h – радиус шара, в котором определена функция Ляпунова □

Доказательство теоремы, а, значит, и предыдущего следствия из теоремы о необходимых и достаточных условиях экспоненциальной устойчивости ЛОСС, завершено.

Не нашли, что искали? Воспользуйтесь поиском: