Обоснование асимптотической и экспоненциальной устойчивости линейных однородных стационарных систем (ЛОСС) с помощью квадратичных форм

Как всегда, отправным результатом второго метода Ляпунова является случай, рассмотренный самим А.М. Ляпуновым в его знаменитом труде [11], а именно, рассмотрим n -мерную линейную однородную стационарную систему (ЛОСС) дифференциальных уравнений вида

(2.3.1)

где А – постоянная вещественная -мерная матрица. Очевидно, что система (2.3.1) допускает тривиальное решение и, таким образом, является частным случаем общей нелинейной нестационарной системы (2.1.1.)÷(2.1.3), рассматриваемой во втором методе Ляпунова.

Из теории устойчивости систем линейных стационарных дифференциальных уравнений [1] известно, что тривиальное решение ЛОСС асимптотически устойчиво по Ляпунову при тогда и только тогда, когда все собственные числа, или, что одно и то же, все корни характеристического многочлена матрицы А вида

(2.3.2)

имеют все (строго) отрицательные вещественные части, т.е.

(2.3.3.)

а так как областью определения ЛОСС является все полупространство , то имеет место асимптотическая устойчивость в целом тривиального решения ЛОСС, а в силу линейности системы (2.3.1), и каждое ее решение будет асимптотически устойчиво в целом [1].

Очевидно, что в силу второй теоремы Ляпунова (об асимптотической устойчивости) (п. 2.1), как следствие, вытекает следующая теорема.

Теорема об асимптотической устойчивости решений ЛОСС. Если для линейной однородной стационарной системы вида (2.3.1) существует функция Ляпунова , удовлетворяющая условиям второй теоремы Ляпунова, то каждое решение этой системы асимптотически устойчиво, а если удовлетворяет, вдобавок, условиям теоремы Барбашина-Красовского, т.е. допускает бесконечный предел в целом (см. п.2.2), то можно говорить об асимптотической устойчивости в целом.■

А.М. Ляпунов доказал, что теорема об асимптотической устойчивости ЛОСС обратима, и указал способ прямого построения положительно определенной функции, фигурирующей в теореме, названным впоследствии способом построения функции Ляпунова по заданной ее производной, вычисленной в силу системы [11,3].

Теорема о необходимых и достаточных условиях асимптотической устойчивости ЛОСС (А.М. Ляпунов, 1892). Пусть дана ЛОСС вида (2.3.1). Для асимптотической устойчивости в целом каждого (в том числе, тривиального) решения ЛОСС, необходимо и достаточно существования не зависящей от времени функции (и допускающей ББНП) Ляпунова , положительно определенной и такой, что ее полная производная, вычисленная в силу ЛОСС, есть независящая от времени отрицательно определенная функция Ляпунова. ■

Доказательство. Зададим функцию Ляпунова в виде вещественной положительно определенной квадратичной формы

(2.3.4)

Замечание. Квадратичная форма (2.3.4) как функция Ляпунова допускает бесконечный предел в целом ■.

Вычислим полную производную в силу системы (2.3.1):

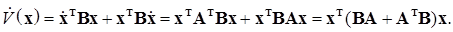(2.3.5)

Заметим, что в (2.3.5) -матрица

симметрична по построению и называется симметризованной матрицей матричного произведения .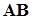

Важным приемом синтеза систем с заданными свойствами устойчивости решений является априорное задание вида полной производной функции Ляпунова, вычисленной в силу системы. В данном случае потребуем, чтобы полная производная имела вид отрицательно определенной квадратичной формы

(2.3.6)

Подставляя (2.3.6) в равенство (2.3.5), приходим к матричному уравнению вида

, (2.3.7)

в котором С – заданная положительно определенная симметричная матрица, В – неизвестная матрица.

Уравнение (2.3.7) называется в математической теории устойчивости матричным уравнением Ляпунова, разрешимость которого исследована А.М. Ляпуновым.

Лемма о разрешимости матричного уравнения Ляпунова (А.М. Ляпунов, 1892)

1. Матричное уравнение Ляпунова (2.3.7) однозначно разрешимо относительно неизвестной матрицы В тогда и только тогда, когда А –гурвицева, то есть характеристический многочлен матрицы А вида

имеет все корни с отрицательными вещественными частями, т.е.

2. Если – отрицательно определённая матрица , то положительно определённая .■

(Без доказательства.)

Утверждение леммы завершает доказательство теоремы. Мы построили (допускающую бесконечный предел в целом) функцию Ляпунова в виде положительно определенной квадратичной формы

удовлетворяющей условиям теоремы, причем матрица В однозначно разрешима из уравнения Ляпунова (2.3.7) по любой наперед заданной симметричной отрицательно определенной матрице тогда и только тогда, когда каждое решение ЛОСС (2.3.1) асимптотически устойчиво в целом. □ (Конец доказательства).

Следствие. Из только что полученного результата о построении функции Ляпунова в виде квадратичной формы по заданной производной, легко вывести следствие: для линейной однородной стационарной системы ЛОСС (2.3.1) асимптотическая устойчивость тривиального решения (а значит, и всех решений) совпадает с экспоненциальной устойчивостью ее тривиального решения (а значит, и всех решений).■

Замечание. Этот результат известен из алгебраической теории линейных однородных стационарных систем и доказывается из анализа формулы Коши для общего решения ЛОСС, записанного с помощью матрицы Коши в виде

удовлетворяющего начальному условию

.■

Замечание. Матричная функция называется экспоненциалом матрицы А.

Докажем приведенное следствие даже в более общей формулировке, обобщая его на нелинейные системы в следующей теореме.

Теорема о достаточных условиях экспоненциальной устойчивости тривиального решения нелинейных систем (Н.Н. Красовский, 1959).

Пусть дана приведенная система общего вида (2.1.1)-(2.1.3)

. (2.3.8)

Если для нее найдется положительно определенная квадратичная форма

(2.3.9)

производная которой , вычисленная в силу приведенной системы (2.3.8), удовлетворяет неравенству

(2.3.10)

где

(2.3.11)

- отрицательно определенная квадратичная форма, то тривиальное решение системы (2.3.8) экспоненциально устойчиво при .■

Не нашли, что искали? Воспользуйтесь поиском: