
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ответ: т.к. , данные прямые параллельны.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
_
Кафедра высшей математики
Векторная алгебра и аналитическая геометрия
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И
ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Москва 2007
С о с т а в и т е л и:
доцент, кандидат физико-математических наукТ.А.Мацеевич
Примеры решения задач по векторной алгебре и аналитической геометрии
Задание №1
Разложить вектор 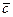 = {9, 4} по векторам
= {9, 4} по векторам 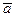 = {2, -3} и
= {2, -3} и 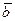 = {1, 2}.
= {1, 2}.
Решение.
Найдем коэффициенты  и
и 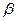 в разложении:
в разложении: 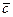 =
= 
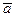 +
+ 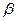
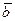 .
.
Запишем эту формулу в координатах. Сначала вычислим координаты правой части:

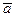 +
+ 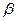
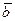 = {2
= {2  ; -3
; -3  } + {1
} + {1 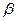 ; 2
; 2 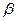 } = {2
} = {2  +
+ 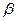 ; -3
; -3  + 2
+ 2 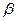 }.
}.
Эти координаты должны равняться соответствующим координатам вектора 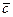 , следовательно:
, следовательно: 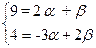 .
.
Решим эту систему уравнений методом исключения переменных.
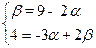

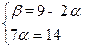

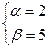
Ответ: 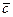 = 2
= 2 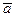 + 5
+ 5 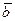 .
.
Задание №2
Проверить коллинеарность векторов 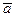 = {2, -1, 3} и
= {2, -1, 3} и 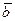 = {-6, 3, -9}.
= {-6, 3, -9}.
Решение.
Если векторы 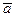 и
и 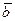 коллинеарны, то их координаты должны быть пропорциональны. Проверим это.
коллинеарны, то их координаты должны быть пропорциональны. Проверим это.
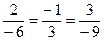 , т.е коэффициент пропорциональности существует и равен
, т.е коэффициент пропорциональности существует и равен 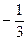 .
.
Ответ: II.
Задание №3
Дан вектор 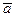 = {2, -1, 3}. Найти модуль вектора
= {2, -1, 3}. Найти модуль вектора 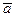 , координаты его орта
, координаты его орта 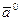 и направляющие косинусы.
и направляющие косинусы.
Решение.
а) Найдем модуль вектора 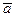 :
:
 .
.
б) Найдем координаты орта 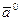 :
:
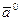 =
=  .
.
в) Найдем направляющие косинусы вектора  :
:
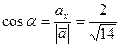 ;
;
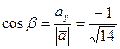 ;
;
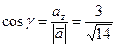 .
.
Ответ:,,,,.
Задание №4
Проверить ортогональность векторов 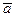 = {-6, -3, 2} и
= {-6, -3, 2} и 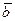 = {1, 2, 6}.
= {1, 2, 6}.
Решение.
Если 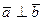 , то их скалярное произведение
, то их скалярное произведение 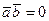 . Найдем
. Найдем 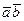 .
.
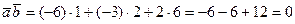 .
.
Ответ:.
Задание №5
Найти угол между векторами 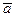 = {3, 0, 4} и
= {3, 0, 4} и 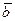 = {7, 0, 1}.
= {7, 0, 1}.
Решение.
Пусть 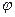 - угол между векторами
- угол между векторами 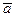 и
и 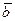 . Тогда
. Тогда
 .
.
Найдем скалярное произведение:
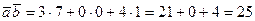 .
.
Найдем модули векторов 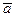 и
и 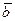 :
:
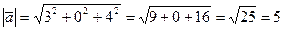 ;
;
 .
.
Найдем 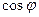 :
:
 .
.
Тогда  .
.
Ответ:.
Задание №6
Найти вектор 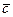 , перпендикулярный векторам
, перпендикулярный векторам 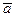 = {2, -2, -3} и
= {2, -2, -3} и 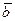 = {4, 0, 6}.
= {4, 0, 6}.
Решение.
Так как 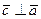 и
и 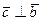 , то
, то 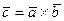 (векторное произведение векторов
(векторное произведение векторов 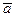 и
и 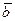 ).
).
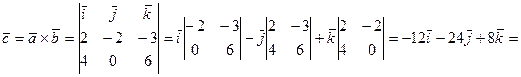 {-12, -24, 8}.
{-12, -24, 8}.
Ответ: {-12, -24, 8}.
Задание №7
Вычислить площадь параллелограмма ABDC и треугольника ABC, если А (0, 2, 2), B (1, -2, 3), C (-1, 2, 1), D (0, -2, 2).
Решение.
Найдем векторы 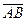 и
и 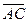 :
:
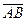 = { 1, -4, 1},
= { 1, -4, 1},
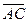 = {-1, 0, -1}.
= {-1, 0, -1}.
Найдем векторное произведение полученных векторов:
 ={4, 0, -4}.
={4, 0, -4}.
Найдем длину полученного вектора
 .
.
Найдем площадь параллелограмма ABDC:
 .
.
Найдем площадь треугольника ABC:
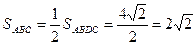 .
.
Ответ:,.
Задание №8
Найти объем пирамиды, вершины которой находятся в точках A(2, -1, 1), B(5, 5, 4),
C(3, 2, -1), D(4, 1, 3).
Решение.
Найдем координаты векторов 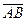 ,
, 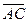 ,
, 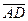 :
:
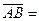 {3, 6, 3},
{3, 6, 3},
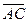 = {1, 3, -2},
= {1, 3, -2},
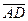 = {2, 2, 2}.
= {2, 2, 2}.
Вычислим смешанное произведение этих векторов:
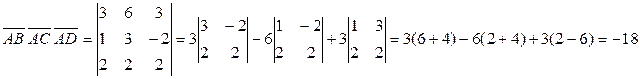
Найдем объем пирамиды:
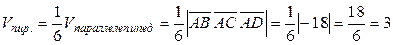 .
.
Ответ:.
Задание №9
Проверить компланарность векторов 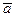 = {2, 3, -1},
= {2, 3, -1}, 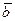 = {1, -1, 3} и
= {1, -1, 3} и 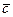 = {1, 9, -11}.
= {1, 9, -11}.
Решение.
Вычислим смешанное произведение векторов 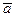 ,
, 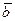 и
и 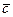 :
:
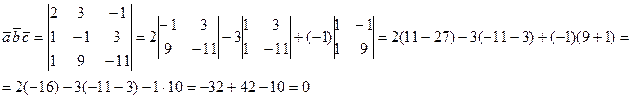
Так как 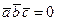 , следовательно, векторы
, следовательно, векторы 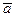 ,
, 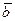 и
и 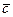 - компланарны.
- компланарны.
Ответ: 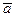 ,
, 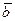 и
и 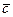 - компланарны.
- компланарны.
Задание №10
Составить общее уравнение прямой, проходящей через точки 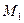 (3; 1) и
(3; 1) и 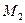 (5; 4).
(5; 4).
Решение.
Подставляя данные координаты точек 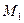 и
и 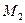 в формулу
в формулу
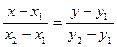 ,
,
получаем искомое уравнение прямой
 ,
,
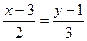 ,
,
 ,
,
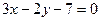 .
.
Ответ:.
Задание №11
Две прямые заданы уравнениями  и
и 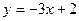 . Найти угол между этими прямыми.
. Найти угол между этими прямыми.
Решение.
Угловые коэффициенты данных прямых:
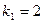
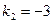 .
.
Поэтому по формуле
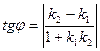 ,
,
находим
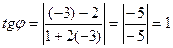 .
.
Таким образом, угол между данными прямыми равен
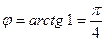 .
.
Ответ:.
Задание №12
Показать, что прямые  и
и 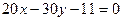 параллельны.
параллельны.
Решение.
При приведении уравнения каждой прямой к виду
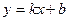
получаем:
 или
или 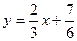 ;
;
и
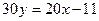 или
или 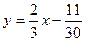 .
.
Откуда видно, что угловые коэффициенты 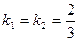 .
.
Следовательно, прямые параллельны.
Ответ: т.к., данные прямые параллельны.
Задание №13
Показать, что прямые 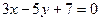 и
и 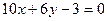 перпендикулярны.
перпендикулярны.
Решение.
Приведя уравнения каждой прямой к виду
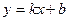
получаем:
 или
или 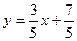 , где
, где 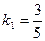 - угловой коэффициент,
- угловой коэффициент,
и
 или
или 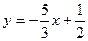 , где
, где 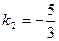 - угловой коэффициент.
- угловой коэффициент.
Откуда видно, что угловые коэффициенты  .
.
Следовательно, прямые перпендикулярны.
Не нашли, что искали? Воспользуйтесь поиском: