Использование матричных операторов для преобразования матриц и векторов

На панели Mатричные расположены операторы, позволяющие выполнять некоторые матричные и векторные преобразования.

Оператор выделения (Х_n) элемента матрицы или вектора позволяет выделить (определить) элемент матрицы или вектора. При выделении элемента следует учитывать, что по умолчанию индексация элементов матрицы и векторов начинается с нуля, например для выделения первого элемента матрицы P необходимо записать:

Для ввода второго индекса, необходимо ввести запятую после первого индекса и затем в появившийся маркер ввести второй индекс массива.

Оператор вычисления обратной матрицы (X^-1) позволяет вычислить обратную матрицу, например:

Кстати, хорошо известно, что если обратную матрицу умножить на обычную, то получается единичная матрица:

Оператор вычисления детерминанта (определителя) матрицы |Х|:

Определитель матрицы, как известно, это число, вычисляемое по матрице по определенным правилам.

Оператор векторизации (). Векторизация означает выполнение однотипной операции с каждым элементом массива, например:

В данном случае вычислен косинус от каждого элемента вектор – столбца p4.

Другой пример: необходимо вычислить десятичный логарифм от заданной матрицы P5.

Оператор выделения вектор столбца матрицы (M^{< >}) позволяет выделить заданный столбец матрицы и записать его в виде вектор – столбца, например, для выделения первого столбца матрицы P4 необходимо выполнить:

Оператор транспонирования (М^Т) матрицы позволяет перевернуть матрицу на 90 градусов так, что столбцы становятся строками:

Транспонирование вектор–столбца позволяет получить вектор – строку:

Оператор вычисления суммы (Συ) вектор–столбца позволяет вычислить сумму элементов вектор-столбца:

Матричные функции

Функция cols() позволяет определить число столбцов матрицы:

Функция rows() позволяет определить число строк массива:

Функция max() позволяет определить максимальный элемент массива:

Функция min() позволяет определить минимальный элемента массива:

Функция mean() позволяет вычислить среднее значение элементов матрицы:

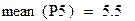
Функция last() предназначена для вычисления индекса последнего элемента вектора:

Максимальное значение индекса вектор-столбца С равно двум, т.к. индексация элементов начинается с нуля.

Для изменения начальной индексации матриц и вектор-столбцов используют специальную системную переменную (ORIGIN) значение которой можно переопределять. Такую переменную, записанную прописными буквами, необходимо поместить над матрицей, индексы которой переопределяются, например:

Вышеприведенная запись означает, что индексация элементов матрицы, расположенной ниже системной переменной, начата с единицы.

Для генерации матрицы произвольных размеров можно использовать функцию rnd (х), позволяющую получить равномерно распределенное случайное число от нуля до x. Сгенерирум квадратную матрицу с элементами, значение которых не превышает 10:

Если использовать функцию округления ceil (x), которая вычисляет наименьшее целое число большое или равное x то получим матрицу с целочисленными элементами:

Задача 12. Найти сумму всех элементов квадратной матрицы. Cформировать целочисленную матрицу, используя функцию rnd (максимальное значение элемента равно десяти).

Программа в MathCad:

ORIGIN:=1

При решении данной задачи следует учитывать, что при использовании функции rnd каждый раз будет получатся новая матрица.

Задача 13. Вычислить сумму отрицательных элементов заданной квадратной матрицы F и найти их и число (количество).

Не нашли, что искали? Воспользуйтесь поиском: