
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
механічна система у стані рівноваги займає той стан, який має мінімальну по відношенню до найближчих станів потенціальну енергію.
Примітка. Цей принцип для його кращого розуміння можна пояснити на простому прикладі. М’яч, покладений на нерівну поверхню, знайде своє положення рівноваги у локальному мінімумі (заглибині), яка дозволить йому мати потенціальну енергію меншу, ніж у будь-якій із найближчих точок цієї поверхні).
Мінімум потенціальної енергії може бути не загальним, а локальним, тобто по відношенню до найближчої ділянки простору. У будь-якому разі – це той стан, у якому градієнт потенціальної енергії (а отже, і сила, що діє на тіло або систему) дорівнює нулю. Слід додати, що може бути також інший (нестійкий) стан рівноваги механічної системи, в якому потенціальна енергія має локальний максимум. Але прийти до цього стану під дією лише потенціального поля сил механічна система не може, оскільки ці сили завжди спрямовані не до локального максимуму, а в протилежному напрямі.
3. Кінетична енергія
Крім потенціальної енергії, зумовленої взаємодією механічної системи з певним силовим полем, вона може мати ще один вид механічної енергії, пов’язаної з рухом системи. Ця енергія називається кінетичною.
Визначимо залежність кінетичної енергії від параметрів руху тіла.
Запишемо для деякого тіла ІІ-й закон Ньютона:
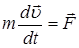 . .
| (17) |
Переміщення тіла:
 . .
| (18) |
Перемножимо ці два рівняння скалярно (ліву частину на ліву і праву – на праву):
 . .
|
Перетворимо ліву частину цього рівняння:
  . .
|
Отже,
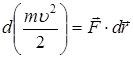 . .
| (19) |
У лівій частині під знаком диференціала стоїть величина
 , ,
| (20) |
яка називається кінетичною енергією тіла.
Кінетичною називається енергія, яку механічна система має внаслідок свого руху.
У правій частині (19) – вже відомий нам вираз  , що дорівнює dA (роботі сили
, що дорівнює dA (роботі сили  на переміщенні
на переміщенні  ).
).
Отже, згідно з (19),
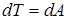 , ,
|
Тобто при виконанні роботи над певним тілом на таку саме величину змінюється його енергія.
Робота – це величина зміни енергії.
Якщо відома енергія системи до виконання роботи і енергія після виконання роботи, то робота дорівнює різниці цих енергій. Це дозволяє в ряді випадків уникати складних розрахунків за формулою (3) і отримувати результат значно простіше.
Наприклад, тіло може набути потенціальної енергії в полі сили тяжіння за рахунок роботи, виконаної силою, що підіймає тіло на певну висоту. Але той самий результат можна отримати, якщо тіло рухалося з певною швидкістю, спрямованою вгору. Тоді воно підійметься на ту саму висоту без дії будь-яких сил, а лише за рахунок запасу кінетичної енергії, яка в кінцевому стані перетворюється на потенціальну.
Кінетична енергія визначається за формулою (20) для матеріальної точки, а також для будь-якого тіла, яке рухається поступально. У деяких випадках може бути корисною й інша формула для кінетичної енергії тіла, що рухається поступально – через імпульс тіла p = mu:
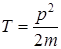 . .
| (21) |
У випадку обертального руху необхідно користуватися іншим співвідношенням. Розглянемо обертання матеріальної точки масою т по коловій траєкторії радіуса r навколо нерухомої осі z з кутовою швидкістю w. ЇЇ кінетична енергія:
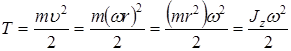 , ,
|
де  – момент інерції матеріальної точки відносно осі обертання z.
– момент інерції матеріальної точки відносно осі обертання z.
Можна довести, що ця формула справедлива і для твердого тіла, що обертається навколо певної осі z:
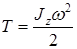 . .
| (22) |
Якщо тіло одночасно бере участь і в поступальному, і в обертальному рухах (наприклад, циліндр, що скочується з похилої площини), то для визначення його загальної кінетичної енергії необхідно знайти суму кінетичних енергій кожного з цих рухів. При цьому при визначенні кінетичної енергії поступального руху слід розглядати рух центру мас тіла, а для визначення кінетичної енергії обертального руху – обертання навколо осі, що проходить через центр мас:
 . .
| (23) |
Отже, рух будь-якої механічної системи в потенціальному силовому полі характеризується енергіями 2 типів – кінетичною і потенціальною.
Як підсумок, можна дати такі визначення різних типів механічної енергії.
Потенціальною називається енергія механічної системи, зумовлена її взаємодією з певними силовими полями, яка залежить від просторового положення системи та її частин.
Кінетичною називається енергія, яку механічна система має внаслідок свого руху.
Сума кінетичної й потенціальної енергій називається повною механічною енергією системи:
| Е = Т + П. | (24) |
Необхідно завжди пам’ятати, що робота, виконана над механічною системою, змінює її енергію на величину, що дорівнює виконаній роботі.
Робота дорівнює величині зміни повної енергії системи.
Цей висновок необхідно застосовувати при розв’язуванні багатьох задач.
ЗАВДАННЯ НА САМОПІДГОТОВКУ:
1. Опрацювати конспект лекції 1/5.
2. Повторити методику розв’язування задач, виконаних під час лекцій.
3. Виноградов А.Г. Загальна фізика § 1.6.
Вивчити теоретичний матеріал.
Дати відповіді на контрольні запитання.
| <== предыдущая лекция | | | следующая лекция ==> |
| видовження тіла при деформації пропорційне величині деформуючої сили. | | | Імпульс замкненої механічної системи зберігається(не змінюється з часом), які б процеси не відбувалися всередині системи. |
Не нашли, что искали? Воспользуйтесь поиском: