Рівняння Шредінгера

Для аналізу процесів усередині атома та інших квантових систем необхідно мати теорію механіки мікрочастинок, яка дозволяла б теоретично визначати стан їх руху (координати, імпульси, енергію) в залежності від часу та від певних зовнішніх умов. У той же час, після відкриття хвильових властивостей мікрочастинок та встановлення співвідношення невизначеностей стало очевидним, що класична механіка для розв’язання цієї задачі є непридатною. В її основі лежать рівняння руху, які приводять до точних значень координат та імпульсів частинок, а це, як на той час уже стало зрозумілим у світлі останніх відкриттів, не може дати адекватний опис процесів у мікросвіті. Необхідно було створити зовсім нову механіку, здатну пояснити вже відомі факти і прогнозувати напрямки для нових досліджень.

Основи нової теорії, яка отримала назву “квантова механіка”, були створені у 20-ті роки ХХ століття завдяки зусиллям ряду фізиків-теоретиків, перш за все Е. Шредінгера, В. Гайзенберга і П. Дірака.

У класичній механіці для визначення стану руху певної механічної системи складаються рівняння руху на основі ІІ закону Ньютона, до яких входять координати цієї системи та їх похідні по часу (швидкості і прискорення), зв’язані між собою певною функціональною залежністю. Після розв’язання системи таких рівнянь можна отримати залежність координат від часу і з цієї залежності отримати всі інші параметри системи (швидкість, прискорення, імпульс, енергію тощо) в залежності від часу.

У квантовій механіці рівняння, що визначають стан системи, складаються не відносно координат та їх похідних, а відносно деякої функції, яка є головною характеристикою квантової системи і яка називається хвильовою функцією. Хвильова функція залежить від координат квантової системи і від часу:

.

Якщо необхідно визначити стан певної мікрочастинки (наприклад, електрона), то треба знайти відповідну хвильову функцію і, знаючи її, можна відповісти на ряд питань про параметри руху цього електрона.

За допомогою хвильової функції можна визначити як хвильові, так і корпускулярні властивості мікрочастинки. Причому вона дає не абсолютні значення певних параметрів, а лише їх імовірність. Наприклад, імовірність того, що мікрочастинка знаходиться у певному елементі простору об’ємом dV:

. (5.21)

Звідси можна зробити висновок, що квадрат модуля хвильової функції, обчислений для певних координат і моменту часу, дорівнює густині ймовірності знаходження мікрочастинки у даній точці простору:

.

Отже, фізичний смисл має не сама хвильова функція, а квадрат її модуля.

Для того, щоб визначити імовірність знаходження даної мікрочастинки в певній ділянці простору об’ємом V, необхідно обчислити інтеграл:

. (5.22)

Для знаходження хвильової функції певної мікрочастинки необхідно скласти рівняння, яке повинно враховувати умови, під впливом яких перебуває ця частинка. Це рівняння у квантовій механіці грає таку саму роль, як і ІІ закон Ньютона – у класичній механіці.

Основне рівняння квантової механіки має назву рівняння Шредінгера, оскільки його вперше запропонував у 1926 році австрійський фізик Е. Шредінгер. Він прийшов до цього рівняння шляхом аналізу відомих на той час експериментальних даних і теоретичних моделей та намагаючись створити таку нову теорію, яка не відкидала б класичну механіку, а містила її як граничний випадок.

Загальне рівняння Шредінгера для мікрочастинки має такий вигляд:

, (5.23)

де т – маса мікрочастинки,

U (x, y, z, t) – її потенціальна енергія,

і – уявна одиниця (),

D – оператор Лапласа (сума других похідних по декартових координатах):

.

Дію оператора Лапласа на хвильову функцію можна написати в такому вигляді:

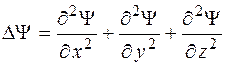. (5.24)

Загальне рівняння Шредінгера (5.23) є справедливим у будь-яких випадках, але воно не завжди є зручним для аналізу квантових систем, оскільки з математичної точки зору воно є складним для розв'язування.

У ряді випадків рівняння Шредінгера намагаються спростити, використовуючи ті чи інші особливості квантових систем.

Досить типовим випадком є такий, коли зовнішнє силове поле, яке визначає потенціальну енергію мікрочастинки, є стаціонарним (сталим у часі). У цьому випадку вираз для потенціальної енергії, який входить до рівняння Шредінгера, не містить залежності від часу:

U = U (x, y, z). (5.25)

Математично доведено, що розв’язок рівняння Шредінгера такого типу приводить до хвильової функції у вигляді добутку двох множників, один із яких залежить від координат, а другий – від часу:

, (5.26)

де w – циклічна частота хвилі, пов’язаної з даною мікрочастинкою (хвилі де Бройля). Згідно з (5.13):

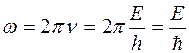. (5.27)

Якщо підставити добуток двох множників (5.26) замість хвильової функції Y в загальне рівняння Шредінгера (5.23), то після виконання математичних операцій множник e ^{– iw t} можна скоротити, і рівняння буде містити лише координатну частину хвильової функції y (x, y, z). При цьому рівняння Шредінгера набере такого вигляду:

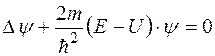. (5.28)

Це – рівняння Шредінгера для стаціонарних станів. Воно має розв’язки не для кожного значення енергії Е, а лише для деяких фіксованих значень, кожне з яких відповідає певному стаціонарному стану квантової системи (мікрочастинки). Ці значення енергії називаються енергетичними рівнями. Кожний стаціонарний стан характеризується своєю координатною хвильовою функцією y (x, y, z), яку можна визначити з рівняння (5.28) після підстановки в нього відповідного значення енергії Е. Повна хвильова функція (5.26) буде визначена після множення координатної функції на залежний від часу множник e ^{– iw t}, в якому циклічна частота знаходиться із співвідношення (5.27):

. (5.29)

Теорія атома водню

Як приклад застосування рівняння Шредінгера до аналізу властивостей конкретної квантової системи, розглянемо одну з найпростіших таких систем – атом водню, тобто атомне ядро (протон) і електрон, зв’язані силою електричного поля.

Будемо розглядати рух електрона у сферичній системі координат, прив’язаній до атомного ядра. Потенціальна енергія взаємодії електрона з ядром – це енергія, що визначається кулонівським потенціалом точкового заряду:

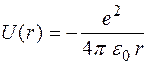, (5.41)

де r – відстань між електроном і ядром (радіус орбіти електрона). Графік цієї функції представлений на рис. 5.5.

Оскільки потенціальна енергія не залежить від часу, можна застосувати рівняння Шредінгера для стаціонарних станів (5.28):

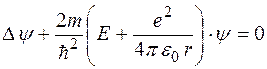, (5.42)

де Е – повна енергія електрона.

Математичний аналіз цього рівняння показує, що воно має розв’язки лише за умови, що енергія електрона дорівнює одному з таких значень:

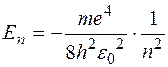, (5.43)

де п = 1, 2, 3,... – ціле число.

Отже, електрон у атомі може мати лише певні дискретні значення енергії (енергетичні рівні), які визначаються співвідношенням (5.43). На рис. 5.6 схематично зображена система енергетичних рівнів атому водню разом із залежністю U (r). Оскільки повна енергія електрона дорівнює сумі його потенціальної і кінетичної енергій Е = U + T ³ U, то на цій діаграмі точка, що зображує енергетичний стан електрона, не може знаходитися нижче від графіка U (r). Тому довжина риски, що зображує певний енергетичний рівень на рис. 5.6, дорівнює максимальному розміру відповідної електронної орбіти у масштабі осі r. Втім, не слід забувати про те, що у квантовій системі точно визначити електронну орбіту неможливо. Можна вказати лише імовірність того, що електрон перебуває в певних просторових межах. Для атома найбільш високою імовірністю перебування електрона характеризуються якраз орбіти певних розмірів і форми, які визначають “електронну хмарину” (розподіл у просторі густини імовірності, визначеної хвильовою функцією електрона (див. (5.20)).

Згідно із загальним принципом, будь-яка механічна система у стані рівноваги займає стан із мінімальним значенням енергії. Це значить, що основним станом атому водню є стан, якому відповідає найнижчий з усіх можливих енергетичний рівень Е ₁ (п = 1). Всі інші стани атому є збудженими. Для того, щоб перевести атом із основного стану в один із збуджених, необхідно надати йому енергію, яка відповідає різниці відповідних енергетичних рівнів. Атом не може довго перебувати у збудженому стані. Через деякий час, який визначається законами квантових систем, атом повертається із збудженого в основний стан, віддаючи відповідну енергію у вигляді кванта електромагнітного випромінювання, який випромінюється у навколишній простір.

Електронна орбіта, що відповідає основному стану атома, має найменші розміри (на рис. 5.6 – r ₁). При зростанні номерів орбіт зростають і їх розміри (r ₂, r ₃, r ₄ і т.д.). При E < 0 електрон знаходиться у зв’язаному стані, тобто він не може подолати силу притягнення до ядра і покинути атом. Цьому діапазону енергій відповідають дискретні енергетичні рівні і обмежені електронні орбіти.

Якщо E ³ 0 – рух електрона не обмежений у просторі. Його енергія є достатньою для того, щоб покинути атом і відлетіти на будь-яку відстань. Цьому діапазону енергій відповідає суцільний енергетичний спектр, тобто для електрона є можливим будь-яке значення енергії E ³ 0 (на рис. 5.6 заштриховано).

Атом, що втратив один або кілька електронів, називається іоном. Зрозуміло, що атом водню може втратити лише один електрон. Для того, щоб атом водню, який перебуває в основному стані, перетворити на іон, його електрон необхідно перевести з першого енергетичного рівня на рівень E ³ 0 (відірвати електрон). Найменша енергія, необхідна для цього – це різниця енергій нульового рівня E = 0 і основного рівня E ₁:

Е_і = 0 – Е ₁ = – Е ₁.

Ця енергія називається енергією іонізації атома. Для атома водню енергія іонізації:

Е_і = – Е ₁ = » 13,55 еВ. (5.44)

Співвідношення для енергетичних рівнів (5.43) співпадає з раніше отриманим співвідношенням на основі постулатів Бора. Але для його отримання не знадобилося використовувати постулати Бора. Співвідношення (5.43) отримане в результаті розв'язування рівняння Шредінгера для даної квантової системи (атома водню).

Таким чином, при застосуванні до аналізу стану атома (як і будь-якої іншої квантової системи) послідовної квантової теорії, в основі якої лежить рівняння Шредінгера, немає необхідності застосовувати постулати Бора. Ці постулати були свого часу введені (фактично – вгадані) для пояснення властивостей атома у світлі досліджень Резерфорда. Але після створення квантової механіки на основі рівняння Шредінгера необхідність у постулатах Бора відпала.

Не нашли, что искали? Воспользуйтесь поиском: