Квантові числа електронів у атомі

Силове поле, що зумовлює рух електрона в атомі водню (електростатичне поле кулонівської взаємодії), є сферично симетричним (залежить тільки від радіусу орбіти r і не залежить від напрямку). Потенціальна енергія електрона (5.41) також є сферично симетричною. Тому і хвильові функції електрона в атомі водню, які є розв’язками диференціального рівняння Шредінгера (5.42), мають сферичну симетрію. У зв’язку з цим, при розв’язуванні даного рівняння використовують не декартову, а сферичну систему координат і отримують хвильові функції, які залежать від координат r, q і j:

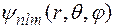. (5.45)

Вигляд функціональної залежності визначається трьома індексами – цілочисельними параметрами n, l і m, кожному набору яких відповідає своя хвильова функція, яка визначає відповідний стан електрона в атомі. З точки зору математики, кожна з цих функцій входить до множини власних функцій диференціального рівняння (5.42).

Цілочисельні параметри n, l і m, які називаються квантовими числами електрона, визначають енергію і момент імпульсу електрона, які він має внаслідок свого руху по орбіті і взаємодії з атомним ядром. Крім того, задавання цих трьох чисел однозначно визначає вигляд хвильової функції, тобто стан електрона в атомі водню.

Головне квантове число n визначає енергетичні рівні електрона в атомі і може набувати будь-яких цілочисельних значень, починаючи з одиниці: n = 1, 2, 3,...

Енергія електрона в атомі водню визначається формулою (5.43) і є дискретною, тобто квантується.

Як показує аналіз рівняння Шредінгера (5.42), момент імпульсу електрона також квантується, тобто може набувати лише певних дискретних значень, які визначаються двома іншими квантовими числами l і m.

На відміну від енергії, яка є скаляром і для визначення якої досить одного квантового числа п, момент імпульсу є вектором, а тому для його визначення необхідно задати два квантових числа, одне з яких визначає його модуль, а інше – напрямок у просторі.

Орбітальне квантове число l визначає модуль орбітального моменту імпульсу електрона, який він має внаслідок свого руху по орбіті навколо ядра. При заданому п орбітальне квантове число може набувати таких цілочисельних значень:

l = 0, 1, 2,..., (n – 1). (5.46)

Модуль орбітального моменту імпульсу електрона для певного значення орбітального квантового числа l можна визначити за допомогою співвідношення:

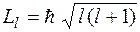. (5.47)

Просторова орієнтація моменту імпульсу визначається по відношенню до існуючого у просторі магнітного поля.

Магнітне квантове число т визначає проекцію орбітального моменту імпульсу електрона на напрямок зовнішнього магнітного поля (напрямок z, рис. 5.7). При заданому l воно може набувати таких цілочисельних значень:

m = – l, – l + 1, …, – 1, 0, 1,..., l – 1, l, (5.48)

тобто всі цілі числа від – l до l, всього 2 l + 1 значень.

З рішень рівняння Шредінгера можна знайти, що проекцію орбітального моменту імпульсу на напрямок зовнішнього магнітного поля (напрямок z) для певного значення магнітного квантового числа т можна визначити за допомогою співвідношення:

. (5.49)

Підсумовуючи все вищесказане, зазначимо, що енергія електрона залежить лише від його головного квантового числа п. З наведених вище співвідношень можна зробити висновок, що кожному значенню енергії (кожному п) відповідає кілька власних функцій y_пlm, які відрізняються значеннями квантових чисел l і m. Це значить, що атом водню може мати одне й те саме значення енергії у кількох різних квантових станах.

Стани з однаковою енергією називаються виродженими, а число різних станів з однаковим значенням енергії називається кратністю виродження відповідного енергетичного рівня.

Кратність виродження G кожного енергетичного рівня з певним значенням п можна легко обчислити, враховуючи можливі значення квантових чисел l і m (див. (5.46) і (5.48)). Оскільки кожному значенню п відповідає п різних значень квантового числа l (від 0 до п – 1), а кожному з цих значень l відповідає 2 l + 1 різних значень квантового числа m, то загальна кратність виродження може бути обчислена як сума ряду:

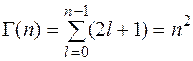. (5.50)

Таким чином, для електрона в основному стані атома водню (п = 1) кратність виродження G дорівнює 1. Справді, при п = 1 можливий лише один набір квантових чисел: l = 0, m = 0.

Для електрона на першому збудженому рівні п = 2 кратність виродження дорівнює 2² = 4. При цьому можливі такі набори квантових чисел l і m:

l = 0, m = 0;

l = 1, m = – 1;

l = 1, m = 0;

l = 1, m = 1.

Аналогічно можна визначити всі можливі комбінації квантових чисел (тобто індексів хвильових функцій) для будь-якого енергетичного рівня.

Для кожного набору квантових чисел існує відповідний розв'язок рівняння Шредінгера – хвильова функція даного квантового стану електрона. Як відомо із сказаного вище (див. “співвідношення невизначеностей”), точні координати та імпульси електрона визначити неможливо внаслідок наявності у нього хвильових властивостей. Тому про електронну орбіту в класичному розумінні цього слова говорити не має сенсу. Електрон не є частинкою, яка рухається вздовж певної траєкторії. Він існує одночасно у всьому об’ємі атома, утворюючи щось на зразок “електронної хмарини”, густина якої пропорційна густині імовірності знаходження електрона в тій чи іншій точці простору.

Густина імовірності дорівнює квадрату хвильової функції (див. (5.21)), а отже, залежить, як і сама функція, від набору квантових чисел.

Квантові числа n і l визначають розмір і форму електронної хмарини, а квантове число m – її орієнтацію в просторі.

В атомній фізиці застосовуються умовні позначення для квантових станів з різними значеннями орбітального квантового числа, при яких кожному значенню l відповідає певна літера латинського алфавіту:

l = 0 – s;

l = 1 – p;

l = 2 – d;

l = 3 – f.

При записі певного стану електрона значення головного квантового числа n записується перед умовним позначенням орбітального числа. Наприклад, запис 2 s означає, що в даному стані n = 2, l = 0.

Отже, рух електрона в атомі навколо ядра визначається трьома квантовими числами n, l і m. Але експериментальні дослідження виявили, що електрону властивий ще один вид руху – внутрішній. Класичним аналогом цього руху є обертання тіла навколо осі, що проходить через його центр мас (так само, як планета Земля, обертаючись по орбіті навколо Сонця, одночасно обертається і навколо власної осі). Внаслідок цього руху електрон має ще один момент імпульсу, не пов’язаний із його рухом навколо ядра атома. Цей власний момент імпульсу електрона, який електрон має завжди, в будь-яких умовах, називається спіном і позначається .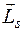

Як і орбітальний момент імпульсу, спін електрона квантується за законом, подібним до (5.47):

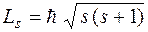, (5.51)

де s – спінове квантове число.

Експериментально було визначено, що для електрона s = 1/2.

Проекція спіну на напрямок зовнішнього магнітного поля визначається співвідношенням, подібним до (5.49):

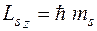, (5.52)

де m_s – магнітне спінове квантове число. Це квантове число для електрона може мати тільки 2 значення:

m_s = ± 1/2. (5.53)

Спін властивий не лише електрону, але й іншим елементарним частинкам: протону, нейтрону, фотону та іншим, а також складним квантовим системам, що складаються з елементарних частинок (ядра, атоми, молекули тощо).

Наявність у електрона додаткового (внутрішнього) ступеня свободи – спіна, приводить до того, що для повного визначення стану електрона в атомі необхідно враховувати і орієнтацію спіна відносно зовнішнього магнітного поля, тобто магнітне спінове квантове число m_s. Оскільки воно може мати два значення (5.53), то число можливих квантових станів, що відповідає певному енергетичному рівню (кратність виродження) необхідно помножити на 2 (див. (5.50)):

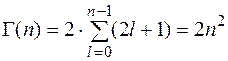. (5.54)

Наприклад, для електрона на першому енергетичному рівні (п = 1) кратність виродження G дорівнює 2. Це два квантові стани, які відрізняються орієнтацією спіна – вздовж магнітного поля і проти поля.

Наведені вище співвідношення та висновки зроблені по відношенню до найпростішого з усіх атомів – атома водню, який має лише один електрон. Але їх можна розповсюдити і на всі інші атоми, що мають велику кількість електронів.

Отже, стан електрона в будь-якому атомі характеризується 4-ма квантовими числами:

головне квантове число n,

орбітальне квантове число l,

магнітне квантове число т,

магнітне спінове квантове число m_s.

Оскільки число можливих квантових станів електрона в атомі, внаслідок необмеженості числа n, є нескінченно великим, виникає питання про те, в яких станах знаходяться всі електрони багатоелектронного атома.

(Не обов’язково)

Не нашли, что искали? Воспользуйтесь поиском: