Генератор псевдослучайной последовательности (ПСП) максимальной длины

Среди сложных сигналов, обладающих хорошими корреляционными свойствами, являются сигналы, формируемые на основе псевдослучайных последовательностей максимальной длины.

Математической основой для описания способов формирования таких последовательностей является представление кодовых комбинаций в виде полиномов от фиктивной переменной x степени n-1, где n – число разрядов комбинации, причем степени членов полинома соответствуют весу разрядов кода.

Если обозначить код в n разрядов как a_n-1, a_n-1… a_1, a₀

то кодовую комбинацию можно представить как полином от фиктивной переменной x a(x)=a_n-1*x^n-1+a_n-2*x^n-2+…+a₁*x¹+a₀*x⁰

Например, кодовой комбинации 100111 соответствует полином a(x)=x⁵+x²+ x¹+1

(Операции над элементами полиномов выполняются по модулю 2).

Основой построения генераторов ПСП также являются регистры сдвига с обрат­ными связями на сумматорах по модулю 2 (схемах исключающих ИЛИ). Такие генера­торы также описываются полиномами g(x) от фиктивной переменной x. Формирующий ПСП полином g(x) и определяет обратные связи генератора на основе регистра сдвига.

Например, полиному g(x)=x⁶+x+1 соответствует регистр на рис.18.

.

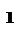
Рис.18. Генератор ПСП. T1…T6 – ячейки регистра сдвига, M2 – сумматор по модулю 2

Очередной символ, вводимый в регистр, определяется как сумма по модулю 2 предыдущих в регистре символов. В данном случае x⁶+x.

Если в качестве порождающего полинома g(x) используется так называемый примитивный полином (делится только на самого себя и на 1), то состояния регистра принимают все возможные двоичные сочетания (кроме нулевого состояния) и формируемая им последовательность двоичных сигналов является последовательностью максимальной длины с периодом повторения N=2^m-1, где m – степень порождающего полинома (число разрядов регистра сдвига).

Примечательным свойством ПСП максимальной длины являются отличные корреляционные свойства (правда, периодические): уровень боковых лепестков АКФ составляет 1/N от основного лепестка.

Такие корреляционные свойства ПСП проявляются при условии, что используются противоположные сигналы: +1 и -1 или сигналы с противофазной ФМ- модуляцией.

Техническая реализация генератора ПСП представлена на рис.19.

(файл «ПСП.CIR»).

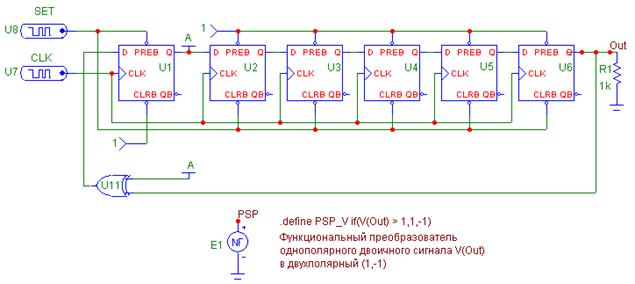
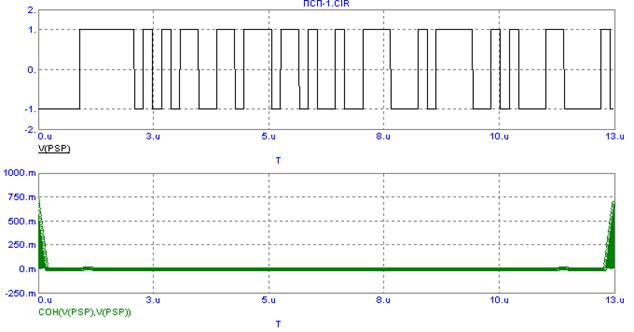
Рис.19. Реализация генератора ПСП (g(x)=x⁶+x+1) и автокорреляционная функция ПСП.

Для анализа корреляционных свойств в Micro-Cap можно воспользоваться функцией:

COH(u,v) – нормированная корреляционная функция сигналов u и v, но для этого следует преобразовать дискретные двоичные сигналы цифрового генератора ПСП в напряжения. Для этой цели на схеме рис.17 и подключен на выходе регистра резистор R1, а для преобразования однополярного напряжения в двухполярное с уровнями +1/-1 включен функциональный преобразователь E1.

Не нашли, что искали? Воспользуйтесь поиском: