Помехоустойчивость двоичного приемника

⇐ Предыдущая 1 2 3 4 5 67

Таким образом, мы получили алгоритм оптимальной обработки сигналов, обеспечивающий наименьшую среднюю вероятность ошибочных решений при приеме сигналов, а также определили структуру устройств, реализующих этот алгоритм для ряда частных случаев приема. То есть, решена задача синтеза устройства на основе оптимизации целевой функции проектирования – минимизации вероятности ошибок.

Следующим шагом является анализ полученного решения - определение качественные показатели приема, то есть определение вероятность ошибок при приеме сигналов для синтезированного приемника (приемников). В процессе анализа также покажем, от чего зависит эта вероятность.

Сначала рассмотрим вариант приемника, который выполняет различение сигналов с одинаковыми энергиями, т.е. ФМ и ЧМ (другие случаи рассмотрим позже).

Итак, пусть

. (3.1)

В этом случае правило приема состоит в формировании пары корреляционных интегралов и их сравнении:

. (3.2)

Будем считать, как и ранее, что сигнал принимается на фоне нормального белого шума (НБШ) со спектральной плотностью .

Для анализа нам понадобится корреляционная функция такого шума. Она является обратным преобразованием Фурье от энергетического спектра шума (теорема Парсеваля) и имеет вид:

. (3.3)

Итак, для приемника, построенного в соответствии с (3.2) правило работы следующее:

В случае если корреляционный интеграл Y ₀> Y ₁принимается решение S^* = S ₀, в том же случае, если Y ₁> Y ₀ - выносится решение S^* = S ₁.

Ошибочные решения возникают в тех случаях, когда на самом деле был передан сигнал S = S ₀(t), но из-за помех получилось, что величина корреляционного интеграла Y ₁> Y ₀и выносится решение S^* = S ₁.

Или же второй вариант - передавался сигнал S = S ₁(t), но помехи привели к тому, что Y ₀³ Y ₁и будет вынесено решение S^* = S ₀(t).

То есть принимаемое решение определяется соотношением между величинами Y ₀и Y ₁.

Для определения вероятности ошибок найдем величины корреляционных интегралов на выходе двух каналов приемника (3.2) Y ₀и Y ₁при передаче сигналов S ₀(t) и S ₁(t).

Корреляционный интеграл Y ₀ при передаче сигнала S ₀(t) будем записывать как Y ₀/ S ₀. Он будет иметь величину:

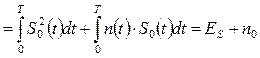. (3.4)

В этом выражении первое слагаемое – это “полезная” часть Y _0,обусловленная сигналом, и равная его энергии.

Второе слагаемое – это “шумовая” часть, которая обусловлена наличием в принятом колебании помехи n (t).

Величина корреляционного интеграла во втором канале приемника - Y ₁ при передаче того же сигнала S ₀(t) будет следующей:

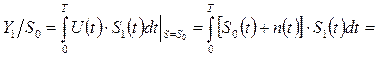
. (3.5)

где R - коэффициент корреляции между сигналами S ₀(t) и S ₁(t)

. (3.6)

В выражении (3.5), также как и ранее, первое слагаемое – это составляющая, обусловленная действием сигнала S₀(t), но уже в противоположном канале Y₁. Поэтому ее величина определяется не только энергией, но и коэффициентом корреляции между сигналами S₀(t) и S₁(t).

Определим те же величины для случая, если передавался сигнал S ₁(t)

(3.7)

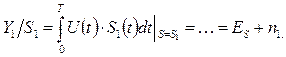. (3.8)

В этих выражениях, E _S - энергия сигнала, одинаковая для обоих сигналов S ₀(t) и S ₁(t); n ₀ и n ₁— шумовые составляющие Y ₀ и Y ₁, обусловленные интегрированием помехи на интервале приема.

Теперь посмотрим, как соотносятся между собой эти величины. Допустим, передан сигнал S ₀(t), т.е. S = S ₀(t).

Тогда величины корреляционных интегралов Y ₀и Y ₁ приемника - различителя примут значения:

Y₀ / S₀ = E + n₀; (3.9)

Y₁ / S₀= R× E + n₁ (3.10)

Ошибка в этом случае произойдет если величина корреляционного интеграла Y ₁> Y ₀, то есть Y ₁ /S ₀> Y ₀ /S ₀или же

E + n ₀< R×E + n ₁. (3.11)

Перенесем случайные величины в левую часть выражения, а неслучайные – в правую:

(n₀- n₁) > (1 - R)× E. (3.12)

То есть, ошибка при приеме сигнала S ₀(t) произойдет в случае, если случайное число (n ₀- n ₁), обусловленное шумами на входе приемника окажется больше некоторого порога величины (1-R)× E величина которого определяется энергией сигнала и его корреляционными свойствами.

Теперь рассмотрим передачу сигнала S ₁(t).

Ошибка в этом случае произойдет, если Y ₁ / S ₁ < Y ₀ / S ₁, или

(n₁ – n₀) > (1 - R)× E (3.13)

Или, что то же самое

(n₀ – n₁) < - (1 - R) × E. (3.14)

Таким образом, в конечном итоге определение вероятности ошибок приема сводится к определению вероятности того, что некоторое случайное число x = (n ₀– n ₁) будет выходить за заданные пределы (границы) Х ₀= (1 - R) × E и Х ₁= - (1- R) × E.

Из общих положений теории вероятности мы знаем, что, для получения вероятности нахождения случайного числа в некоторых пределах (или выхода за пределы), нужно проинтегрировать плотность вероятностей данной случайной величины по этим пределам, то есть

, (3.15)

. (3.16)

Выражения (3.15) и (3.16) поясняются Рис.3.1, где X ₀и X ₁заданные границы, вероятность выхода случайного числа x за которые необходимо найти.

Рис. 14

Таким образом, сначала необходимо определить вид функции распределения p (x) случайной величины x = (n ₀- n ₁).

Случайные величины n ₀и n ₁ представляют собой интегралы (суммы) от нормально распределенного процесса n (t) и, следовательно, также распределены по нормальному закону (согласно центральной предельной теореме).

Можно было бы попытаться определить аналитическое выражение для плотности распределения случайных чисел x = (n ₀- n ₁) и подставить его в (3.15) и (3.16). С учетом нормальности x это не очень сложно.

Но проще воспользоваться тем, что для нормальных величин вероятность превышения порога можно определить по табулированной функции ошибок Ф (z)

Вер (х > X₀) = 1- Ф(z) = 1 - Ф , (3.17)

где m _x - математическое ожидание случайной величины x,

s - среднеквадратическое уклонение x, равное корню квадратному из дисперсии s_x = ,

Ф (z) - табулированный интеграл вероятности (функция ошибок), значения которого можно найти в любом справочнике по математике.

Таким образом, в конечном итоге определение вероятности ошибок сводится к нахождению математического ожидания и дисперсии случайных чисел x = (n ₀- n ₁).

Определим эти величины:

, (3.18)

поскольку .

То есть случайные числа x = (n₀ - n₁) имеют нулевое матожидание. Это упрощает решение задачи.

Теперь найдем величину дисперсии D_x = s²_x

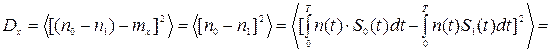
. (3.19)

Выражение в фигурных скобках (3.19) - это корреляционная функция шума n (t). Поскольку прием сигнала ведется на фоне белого шума, то его корреляционная функция имеет вид:

R_n(τ) = . (3.20)

Подставим (3.20) в (3.19). С учетом фильтрующего свойства d -функции двойной интеграл в (3.19) переходит в однократный, и

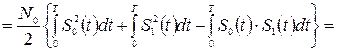
= N₀ × E (1 - R). (3.21)

Среднеквадратическое отклонение x, это корень из дисперсии

s_x = = . (3.22)

Подставив выражения для m _x и s_x в (3.17) окончательно получим вероятность Р _{ОШ 0}, то есть вероятность того, что Y ₁ /S ₀> Y ₀ /S ₀

Р_{ОШ 0} = Вер {п₀- п₁> (1 - R)× E} =
. (3.23)

Точно такое же выражение получится для Р _{ОШ 1}, то есть для случая передачи сигнала S ₁ Y ₀ /S ₁> Y ₁ /S ₁.

Тогда полная вероятность ошибки Р _ОШ = Р ₀ ×Р _{ОШ 0} + Р ₁ ×Р _{ОШ 1}, и для равновероятных сигналов S ₀ и S ₁ будет равна

Р_{ОШ СР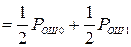} = 1- Ф , (3.24)

где m = E / N ₀ - так называемое энергетическое отношение сигнал/шум

на входе приемника, представляющее собой отношение энергии

полезного сигнала к спектральной плотности белого шума N ₀.

Таким образом, из полученного выражения вероятности ошибок при приеме сигналов мы можем сделать следующий очень важный вывод: качество приема двоичных сигналов определяется всего двумя величинами - энергетическим отношением сигнал/шум на входе приемника и коэффициентом корреляции между различаемыми сигналами.

Чем больше энергетическое отношение сигнал/шум m = E / N ₀ - тем меньше вероятность ошибок.

Чем менее похожи друг на друга (менее коррелированны между собой) сигналы, тем меньше вероятность ошибок.

Рассмотрим несколько частных случаев.

При передаче двоичных сигналов чаще всего используют ортогональные и противоположные сигналы с коэффициентами корреляции между сигналами S ₀(t) и S ₁(t)

равным нулю - R _ОРТ = 0, R _ПРОТ = - 1.

Ортогональными, в частности, являются сигналы при двоичной частотной манипуляции – ЧМн (BFSK). При использовании таких сигналов

Р _ОШ= 1- Ф , (3.25)

При двоичной фазовой манипуляции - ФМн (BPSK), если модуляция производится со сдвигом фазы на π, сигналы противоположны друг другу.

В этом случае

Р_ОШ= 1 - Ф 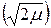. (3.26)

Если для передачи используется пара из нулевого и ненулевого сигналов – этот случай соответствует двоичной амплитудной манипуляции АМн (BASK) вероятность ошибок будет

Р _ОШ= 1 - Ф 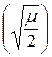. (3.27)

Таким образом, независимо от способа модуляции качественные показатели передачи – средняя вероятность ошибок, определяются одними и теми же выражениями, в которых различается только аргумент функции Ф (z).

При этом для простых видов модуляции АМ, ЧМ и ФМ качество передачи - вероятность ошибок будет при прочих равных условиях наилучшим для ФМ, несколько хуже – для ЧМ, и наихудшим – для АМ.

На Рис. 15 приведен вид функции 1 - Ф (z) (в логарифмическом по оси ординат масштабе)

Рис. 15

На следующем рисунке – Рис. 16 приведены зависимости вероятности ошибок от энергетического отношения сигнал/шум m = E/N ₀ при использовании различных сигналов (противоположных - ФМн, ортогональных – ЧМн, и сигналов типа 0 – 1, что соответствует АМн).

Рис. 16

При постоянной амплитуде сигнала его энергия равна произведению мощности на длительность E = Р _S Т, то большой величины m можно достичь, как увеличением мощности полезного сигнала Р _Sтак и увеличением его длительности Т.

Чтобы пояснить последнее утверждение, умножим и разделим выражение для m на 2FT

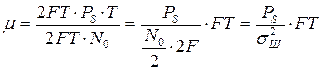. (3.28)

Откуда видно, что m, а следовательно и вероятность ошибок, зависят не только от отношения мощности сигнала к мощности шума, как это обычно принято считать, а еще и от длительности сигнала. Имея отношение сигнал/шум по мощности намного меньше единицы можно, за счет увеличения длительности сигнала, обеспечить очень хорошее m, и, соответственно малую вероятность ошибок.

Контрольные вопросы и задачи:

1. Как, по имеющейся структуре оптимального “аналогового” двоичного приемника получить структуру “цифрового” двоичного приемника?

2. Почему при выводе алгоритма работы цифрового приемника использована модель не “белого” шума, а модель шума с ограниченной полосой (“полосового белого шума”)?

3. Как выглядит корреляционная функция “полосового белого шума”, чему равны ее значения для (t_k – t_l)=0, и (t_k – t_l)≠0?

4. Как выглядит структурная схема “цифрового” двоичного приемника?

5. Запишите условия принятия ошибочных решений при приеме двоичного сигнала.

6. Как условия вынесения ошибочных решений связаны с величинами Y ₀ и Y ₁ на выходах приемника?

7. Как определить вероятность превышения случайной величиной некоторого порога?

8. Как определить вероятность превышения случайной величиной с нормальным распределением некоторого порога?

9. Запишите и поясните общее выражение для вероятности ошибок при двоичном приеме.

10. От каких параметров сигналов и помех зависит вероятность ошибок при двоичном приеме?

11. Объясните зависимость вероятности ошибок при двоичном приеме от длительности сигнала.

12. Объясните зависимость вероятности ошибок при двоичном приеме от коэффициента корреляции между сигналами.

13. Какой из видов двоичной модуляции (АМ, ЧМ или ФМ) обеспечивает лучшую помехоустойчивость и почему?

14. При приеме двоичного сигнала с АМ вероятность ошибок P _ош составляет 10^-3. Как изменится вероятность ошибок, если при прочих равных условиях перейти с АМ на ЧМ или на ФМ?

15. При приеме двоичного сигнала с АМ вероятность ошибок P _ош составляет 10^-4. Насколькоможно уменьшить мощность передатчика системы связи, если, при сохранении вероятности ошибок перейти с АМ на ЧМ (на ФМ)?

16. При приеме двоичного сигнала с ЧМ вероятность ошибок P _ош составляет 10^-5. Во сколько разможно увеличить скорость передачи двоичных символов если, при сохранении заданной вероятности ошибок перейти с ЧМ на ФМ?

17. Спектральная плотность помех на входе двоичного приемника N ₀ /2 равна 10^-15вт/Гц. Ширина полосы приемника 2F _m = 10⁴ Гц. Мощность сигнала на входе приемника - 10^-12 вт.

Какой должна быть длительность сигнала (в секундах) при двоичном приеме и использовании ЧМ, чтобы вероятность ошибок была не более 10^-4?

18. Как изменится эта величина, если с ЧМ перейти на ФМ?

19. Спектральная плотность помех на входе двоичного приемника N ₀ /2 равна 10^-17вт/Гц. Ширина полосы приемника 2F _m = 10⁵ Гц. Мощность сигнала на входе приемника - 10^-8 вт. Длительность символа передаваемых данных – 1 мс. Модуляция – двоичная ЧМ.

Чему равно отношение сигнал/шум по мощности на входе приемника? Чему равна вероятность ошибок при приеме?

Как изменится отношение сигнал/шум по мощности на входе приемника, если полосу приемника расширить до 2F _m = 10⁶ Гц?

Как при этом изменится вероятность ошибок при приеме сигналов?

20. Пользуясь семейством графиков зависимости P _ош (μ) для различных видов модуляции (Рис. 16) определить:

- во сколько раз можно уменьшить мощность передатчика системы связи при переходе с АМ на ЧМ и заданной вероятности ошибок P _ош = 10^-5?

- во сколько раз можно уменьшить мощность передатчика системы связи при дальнейшем переходе с ЧМ на ФМ и заданной вероятности ошибок P _ош = 10^-5?

- найти то же самое, но при заданной вероятности ошибок P _ош = 10^-3?

⇐ Предыдущая 1 2 3 4 5 67

Не нашли, что искали? Воспользуйтесь поиском: