Динаміка твердого тіла

Основні формули

1. Основне рівняння динаміки обертального руху відносно нерухомої осі

,

де – результуючий момент всіх діючих сил;

– вектор моменту імпульсу тіла.

Вектор моменту імпульсу тіла дорівнює

,

де r – радіус-вектор;

mυ – імпульс тіла.

У випадку постійного моменту інерції

,

де – кутове прискорення;

І – момент інерції тіла (міра інертності тіла при обертальному русі).

2. Момент імпульсу тіла, що обертається відносно осі

.

3. Момент сили F, що діє на тіло відносно осі обертання

,

де l – плече сили – найкоротша відстань від осі обертання до лінії дії сили.

4. Момент інерції матеріальної точки відносно нерухомої осі обертання

,

де m – маса точки;

r – відстань від точки до осі обертання.

Момент інерції довільного твердого тіла

де r_i – відстань елемента маси ∆m_i від осі обертання.

Це ж співвідношення в інтегральній формі (для тіл правильної геометричної форми)

.

Якщо тіло однорідне, тобто його густина ρ однакова по всьому об’єму, то

і ,

де V – об’єм тіла.

Теорема Штейнера. Момент інерції твердого тіла або матеріальної точки відносно довільної осі обертання, але обов’язково паралельній до осі, що проходить через центр мас тіла, дорівнює

,

де І₀ – момент інерції цього тіла відносно осі, що проходить через центр мас тіла;

a – відстань між паралельними осями;

m – маса тіла.

5. Закон збереження моменту імпульсу

.

Моменти інерції найпростіших тіл показані в таблиці 1:

Тіло	Вісь, відносно якої визначається момент інер ції тіла	Формула моменту інерції тіла
Однорідний тонкий стрижень масою m і довжиною l	Проходить через центр тяжіння стрижня перпендикулярно до нього
Однорідний тонкий стрижень масою m і довжиною l	Проходить через кінець стрижня перпендикулярно до нього	І =
Тонке кільце, обруч, труба радіусом R і масою m, маховик радіусом R і масою m	Проходить через центр тяжіння перпендикулярно до площини основи	І = mR2
Круглий однорідний диск (циліндр) радіусом R і масою m	Проходить через центр тяжіння перпендикулярно до площини основи	І =
Однорідна куля масою m і радіусом R	Проходить через центр кулі	І =

Таблиця 1

Для двох взаємодіючих тіл закон збереження моменту імпульсу записується так:

,

де І₁, І₂ , ₁, ₂ – моменти інерції і кутові швидкості тіл до взаємодії;

, , , – ті самі величини після взаємодії.

Закон збереження моменту імпульсу для одного тіла із змінним моментом інерції

де І₁і І₂ – початковий і кінцевий моменти інерції;

і – початкова і кінцева кутові швидкості тіла.

6. Робота постійного моменту сили М, що діє на тіло, яке здійснює обертання

де – кут повороту тіла.

7. Миттєва потужність, яка розвивається при обертанні тіла,

.

8. Кінетична енергія тіла, яке здійснює обертальний рух

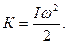
9. Кінетична енергія тіла, яке котиться без ковзання вздовж будь-якої площини

де – кінетична енергія поступального руху тіла;

– швидкість руху центра інерції тіла;

– кінетична енергія обертального руху тіла навколо осі, що проходить через центр інерції.

10. Зв’язок між роботою, яка виконується при обертанні тіла і зміною кінетичної енергії

.

11. Зв’язок між фізичними величинами і формулами, які характеризують поступальний і обертальний рух в найпростіших випадках, показаний в таблиці 2:

Таблиця 2

Поступальний рух	Обертальний рух
Основний закон динаміки
	=
	= І

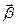
Закони збереження
імпульсу	моменту імпульсу
Робота і потужність
A = Fs	A=M
Кінетична енергія

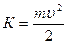
Продовження таблиці 2

Не нашли, что искали? Воспользуйтесь поиском: