Електричне поле у вакуумі

Основні формули

1. Закон Кулона

,

де F – сила взаємодії двох точкових зарядів q₁ і q₂;

r – відстань між зарядами;

– діелектрична проникність середовища;

– електрична стала, яка дорівнює

.

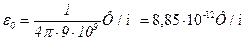2. Закон збереження електричного заряду

,

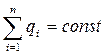де – алгебраїчна сума всіх зарядів, які входять до ізольованої системи.

3. Напруженість електричного поля точкового заряду

,

де – результуючий вектор всіх діючих сил на точковий заряд q, який поміщений в дану точку поля.

Сила, що діє на точковий заряд q, розміщений в електричному полі напруженістю

.

Потік вектора напруженості електричного поля:

а) через довільну поверхню S, яка поміщена в неоднорідне електричне поле,

або ,

де а – кут між напрямком вектора напруженості і нормаллю до елементу поверхні;

dS – площа елемента поверхні;

Е_n – проекція вектора напруженості на напрям нормалі;

б) через плоску поверхню, яка поміщена в однорідне електричне поле,

.

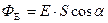4. Потік вектора напруженості Е через замкнену поверхню S дорівнює

,

де інтегрування ведеться через замкнуту поверхню.

5. Теорема Гаусса в інтегральній формі. Потік вектора напруженості електричного поля 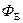через будь-яку замкнуту поверхню дорівнює алгебраїчній сумі зарядів, які охоплені цією поверхнею, поділеній на .

або = ,

де – алгебраїчна сума зарядів, які розміщені в середині замкнутої поверхні;

п – кількість окремих електричних зарядів.

6. Напруженість електричного поля, яке створюється точковим зарядом q на відстані r від заряду

.

7. Напруженість електричного поля, яка створюється зарядженою металевою кулею радіусом R з зарядом q, на відстані r від центра кулі:

- в середині кулі (r < R) – ,

- на поверхні кулі (r = R) – ,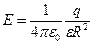

- поза кулею (r > R) – .

8. Принцип суперпозиції (накладання) електричних полів, згідно з яким напруженість результуючого електричного поля, створеного двома (і більше) точковими зарядами, дорівнює векторній (геометричній) сумі напруженостей цих полів:

.

У випадку двох електричних полів з напруженостями _і і ₂ абсолютне значення вектора напруженості дорівнює

,

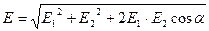де 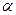– кут між векторами _і і ₂.

9. Напруженість електричного поля, що створюється нескінченно довгою рівномірно зарядженою ниткою (або циліндром) на відстані r від її осі

,

де – лінійна густина заряду.

Лінійна густина заряду визначається відношенням заряду, який розподілений вздовж нитки, до довжини нитки (циліндра):

.

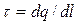10. Напруженість електричного поля, створеного безмежною, рівномірно зарядженою площиною дорівнює

,

де – поверхнева густина заряду.

Поверхнева густина заряду дорівнює відношенню заряду, рівномірно розподіленого на поверхні, до площі цієї поверхні:

.

11. Напруженість електричного поля, яке створюється двома паралельними нескінченними рівномірно і різнойменно зарядженими площинами, з однаковою поверхневою густиною зарядів (поле плоского конденсатора) дорівнює

.

Наведена формула справедлива для обчислення напруженості електричного поля між пластинами плоского конденсатора (в середній його частині) за умови, що відстань між пластинами значно менша лінійних розмірів пластин конденсатора.

12. Електричне зміщення D, з в’язане з напруженістю електричного поля Е таким співвідношенням

.

13. Циркуляція вектора напруженості електричного поля вздовж будь-якого замкненого контуру чисельно дорівнює роботі, яку слід виконати, щоб перемістити одиничний точковий позитивний заряд по цьому контуру.

Циркуляція вектора напруженості виражається коловим інтегралом

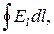
де Е_і – проекція вектора напруженості в даній точці контура на напрямок дотичної до контура в цій самій точці.

У випадку електростатичного поля циркуляція вектора напруженості електричного поля дорівнює нулю:

.

14. Потенціал електростатичного поля – це фізична величина, яка дорівнює відношенню потенціальної енергії в даній точці електричного поля до заряду, який поміщений у цю точку:

.

Або потенціал електростатичного поля – це фізична величина, яка чисельно дорівнює відношенню роботи сил поля для переміщення точкового позитивного заряду з даної точки поля в нескінченність, до величини цього заряду:

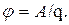
15. Потенціал електростатичного поля у нескінченності умовно приймається за нуль. При переміщенні заряду в електричному полі між точками В і С робота А_ВС зовнішніх сил дорівнює за абсолютним значенням роботі А_СВ

.

Потенціал електростатичного поля, який створюється точковим зарядом q на відстані r від заряду дорівнює:

.

16. Потенціал електричного поля, який створюється зарядженою суцільною металевою кулею радіусом R і зарядом q на відстані r від кулі дорівнює

- в середині кулі (r < R) – ,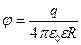

- на поверхні кулі (r = R) – ,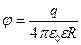

- поза кулею (r > R) – .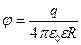

17. Потенціал електростатичного поля, яке створене системою n точкових зарядів, визначається в даній точці поля за принципом суперпозиції і дорівнює алгебраїчній сумі потенціалів 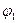, ,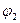..., , які створюються окремими точковими зарядами q₁, q₂,..., q_n

.

18. Енергія W взаємодії системи точкових зарядів q₁,q₂,...,q_n визначається роботою, яку ця система зарядів має виконати за умови перенесення кожного із зарядів, один відносно одного, у нескінченність і виражається формулою

,

де _і – потенціал поля, яке створюється усіма п-1 зарядами (за виключенням і-го) у точці, де розміщений заряд q_і.

19. Потенціал пов'язаний із напруженістю електричного поля співвідношенням

.

У випадку електричного поля, яке має сферичну симетрію, цей зв'язок виражається формулою

або в скалярній формі

,

а у випадку однорідного поля, тобто поля, напруженість якого у кожній точці поля однакова

,

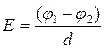де d – відстань між цими поверхнями вздовж електричної силової лінії.

20. Робота, яка виконується електричним полем при переміщенні точкового заряду із однієї точки поля з потенціалом 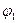в іншу з потенціалом 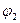, дорівнює

або ,

де 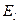– проекція вектора напруженості на напрямок переміщення;

dl – переміщення.

У випадку однорідного поля остання формула набуває вигляду

де l – переміщення;

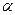– кут між напрямами вектора і переміщення l.

Не нашли, что искали? Воспользуйтесь поиском: