
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методи кореляційно-регресійного аналізу.
Методи кореляційно-регресійного зв’язку використовують в економічному аналізі для виявлення форми та щільності зв’язку між різними параметрами досліджуваного об’єкта, характер функціональної залежності між якими невизначено. Найчастіше цей зв’язок є стохастичним. Кореляція виражає імовірнісну залежність між змінними параметрами алгоритму зв’язку. Кореляційна залежність може бути виявлена як між двома кількісними ознаками (парна кореляція), так і між багатьма (множинна кореляція).
Основна умова кореляційно-регресійного аналізу – забезпечити репрезентативності даних, обґрунтованість застосування до досліджуваного явища відповідних імовірнісних схем, що практично зводиться до вибору рівняння відповідної кривої (параболи чи гіперболи) та ін. Отже, на першому етапі визначають показники-фактори кореляційного зв’язку, які достатньо корельовані у зміні досліджуваного показника. Визначивши вид рівняння, розраховують його параметри за вихідними даними методом найменших квадратів. На другому етапі визначають щільність зв’язку результативного показника з показниками-факторами. Ця щільність виражається коефіцієнтами парної чи множинної кореляції. Значення коефіцієнтів показує, яка ймовірність зміни результативного показника, якщо показник-фактор змінити на один пункт.
Залежність досліджуваного показника від одного фактора у найбільш спрощеному вигляді можна виразити алгоритмом:
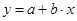 .
.
Для визначення параметрів а і b використовують метод найменших квадратів, який полягає у розв’язанні системи рівнянь:
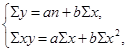
де n – кількість спостережень;
y – результативний показник;
x – факторний показник;
a i b – сталі значення.
Коефіцієнт парної кореляції (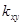 ) визначають за формулою:
) визначають за формулою:

де 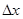 – відхилення від середньої ряду значень показника х;
– відхилення від середньої ряду значень показника х;
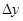 – відхилення від середньої ряду значень показника у.
– відхилення від середньої ряду значень показника у.
Складніші залежності можуть бути виражені рівнянням множинної лінійної кореляції:

Коефіцієнт множинної кореляції (М) визначається так:

де 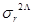 – дисперсія значень величини у, при підстановці взятих зі
– дисперсія значень величини у, при підстановці взятих зі
спостережень значень факторів х у знайдене рівняння
регресії  ,
,
 – дисперсія фактичних значень величини у.
– дисперсія фактичних значень величини у.
Рівняння регресії визначають та розв’язують, використовуючи спеціальні програми для ЕОМ. У завдання аналітика входить формування задачі аналітичного дослідження та правильна інтерпретація її розв’язків. Якщо логічно аналітик може досить ефективно оцінити значущість розв’язку, то побудова рівняння регресії значно спрощується.
На базі методі кореляційно-регресійного зв’язку сформовано економіко-математичний метод аналізу – метод виробничої функції.
Методи математичного програмування призначені для оптимізації господарської діяльності. Цінність їх полягає в тому, що вони дають змогу оцінювати ступінь досягнення потенціалу, визначити лімітуючі ресурси, “вузькі місця”, ступінь конкурентності та дефіцитності.
Не нашли, что искали? Воспользуйтесь поиском: