
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методи обслуговування операцій та економічної кібернетики в аналізі.
У складі інших економіко-математичних методів і моделей можна виділити математичну теорію гри, математичну теорію масового обслуговування, теорію нечітких множин.
Таблиця 2
Модель ключової матриці базових показників
виробничо-господарської діяльності підприємства
| Показники | Випуск продукції (В) | Обсяг основних засобів (З) | Кількість працівників (П) | Матеріальні витрати (М) |
| Випуск продукції (В) | 
| 
| 
| |
| Обсяг основних засобів (З) | 
| 
| 
| |
| Кількість працюючих (П) | 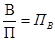
| 
| 
| |
| Матеріальні витрати (М) | 
| 
| 
|
Математичну теорію гри використовують тоді, коли вибирають найвигідніші управлінські рішення, при організації статистичного спостереження і контролю, при організації господарських взаємовідносин з партнерами та в інших ситуаціях. В управлінні ця теорія набула форми ділової гри. Сформулювавши конфліктні ситуації, математично їх можна подати як гру двох, трьох чи більше партнерів, кожен з яких має за мету максимізувати свою вигоду за рахунок іншого партнера. Розв’язуючи такі задачі визначають умови гри: кількість партнерів і правила гри, можливі стратегії партнерів, можливе отримання вигоди. Важливим є сукупність правил гри, за якими залежно від ситуації вибір партнера буде однозначним. Кількість стратегій може бути скінченою і нескінченою. Дослідження стратегій будується на використанні математичного апарату (лінійних рівнянь і нерівностей, ітераційних методів тощо). Якщо виграш одного партнера дорівнює програшу іншого, то їх алгебрична сума дорівнює нулю. Ці ігри називають нульовими. Кожній стратегії відповідає певний виграш (+), або програш (-), залежно від обраної супротивником стратегії. Відповідну інформацію можна подати у вигляді матриці. Наприклад, у парній грі (табл. 3) умови гри містять у собі можливі стратегії кожного партнера і суми виграшу чи програшу для будь-якого поєднання стратегій. Партнер А має три, а партнер Б – чотири стратегії. У табл. 1.13 наведено тільки суми виграшу гравця А, бо для гравця Б ця сама сума буде програшем. Які ж стратегії краще обирати партнерам? Партнер А при стратегії А1 може виграти 10 одиниць, при стратегії А2 - 9, а при стратегії А3 - 11. Але за теорією гри треба вважати, що другий партнер обиратиме стратегії, які дадуть партнерові А не найбільший, а найменший виграш. Такими при стратегії А1 є 3 одиниці, при А2 - 5 і при А3 - 1 одиниця.
Таблиця 3
Умови гри
| Стратегія партнера А | Стратегія партнера Б | Мінімальний виграш партнера А | |||
| Б1 | Б2 | Б3 | Б4 | ||
| А1 А2 А3 | |||||
| Максимальний виграш партнера Б | х |
Якщо врахувати, що партнер А дуже обережний, то на найбільші виграші він не орієнтується. Він думає так: якщо я оберу стратегію А2, то гарантуватиму собі виграш не менше 5 одиниць, а при інших він може бути меншим. Ось ця стратегія партнера А і буде оптимальною. Партнер Б при будь-якій стратегії буде у програші, але програвати він намагатиметься якомога менше. Такою стратегією є Б1, при якій більше 5 одиниць він не програє. Він і обирає цей мінімакс. Партнер А орієнтується на максимін, а партнер Б – на мінімакс. У цій грі їхня тактика збігається і такий збіг називають сідловою точкою. Значення сідлової точки визначає ціну гри.
У теорії гри розглядають і складніші задачі, які виникають через збіг суми виграшу та програшу, при виникненні домовленостей (кооперативні ігри), при непостійній кількості учасників гри, при грі з випадковим результатом та ін.
Математичну теорію масового обслуговування використовують при розв’язку соціально-економічних задач, пов’язаних з організацією обслуговування та ремонту устаткування, проектуванням потокових ліній, планування маршрутів міського транспорту, організацією телефонної служби тощо. Задача теорії масового обслуговування – визначити такі характеристики системи, які забезпечують задану якість її функціонування. Основними елементами системи масового обслуговування, які характеризують структуру, склад і функціональні зв’язки, є вхідний потік запитів, послідовність запитів, засоби обслуговування і вихідний потік запитів.
За строком перебування запитів у системі до початку обслуговування системи масового обслуговування поділяють на три групи: з необмеженим часом очікування, з відмовами (втратами) і змішаного типу. У першому випадку, якщо всі засоби обслуговування зайняті, елемент системи, що надійшов, чекає доти, доки один з них не звільниться. У системах з відмовами будь-який елемент, що надійшов і застав усі засоби зайнятими, виходить із системи. У системах змішаного типу елемент, що надійшов до неї і застав усі засоби зайнятими, перебуває обмежений час, за який або буде обслужений, або залишить систему. Прикладом такої системи є телефонна станція.
До завдань теорії масового обслуговування належать:
· знаходження залежностей, які характеризують якість функціонування обслуговування залежно від характеристик вхідного потоку;
· знаходження параметрів, які характеризують можливості обслуговування;
· вибір способу організації системи загалом.
Задачі теорії масового обслуговування можна розв’язати, використовуючи широку мережу потужних ЕОМ. У випадку, коли система масового обслуговування дуже складна і її треба розв’язати без спрощень, використовують певний імітаційний метод, що потребує значних витрат машинного часу.
Метод дослідження операцій використовують в аналізі для отримання порівняльної оцінки альтернативних рішень. Його мета об’єктивна оцінити пропоновані цілеспрямовані дії і, можливо, пропонування альтернативних варіантів. Складність методу полягає у тому, що досліджувані цілеспрямовані дії (операції), не ізольовані, а пов’язані з іншими діями, які дослідника у цей час не цікавлять, однак можуть впливати на хід операції. Усвідомлення операції, її мети, аналіз факторів, які стосуються цієї мети, порівняння витрат і результатів повинні дати аналітику підставу відмежувати найважливіше і сформулювати умови задачі. При формулюванні умов задачі проводиться добір показників.
Вибором показників і їх формалізацією, визначенням допустимої області зміни та побудовою цільової функції починається другий етап дослідження операцій – перехід від описової моделі до формальної.
Надалі здійснюється аналіз моделі, здебільшого, шляхом статистичного моделювання, за допомогою експертних оцінок, ділових ігрових імітацій тощо.
Не нашли, что искали? Воспользуйтесь поиском: