Модели соединений систем

Для построения моделей соединений систем в Matlab используются знаки арифметических действий. Эти операции перегружены, то есть, переопределены специальным образом для объектов классов tf, ss и zpk. Введем исходные модели, с которыми будем выполнять все операции:

>> f = tf(1, [1 1]);

>> g = tf(1, [2 1]);

· параллельное соединение

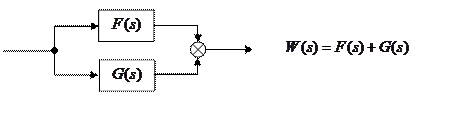
>> w = f + g

Transfer function:

3 s + 2

---------------

2 s^2 + 3 s + 1

· последовательное соединение

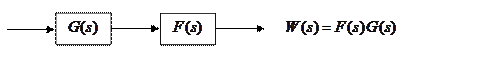
>> w = f * g

Transfer function:

---------------

2 s^2 + 3 s + 1

· контур с отрицательной обратной связью

>> w = feedback(f, g)

Transfer function:

2 s + 1

---------------

2 s^2 + 3 s + 2

Можно вычислить эту передаточную функцию и так:

>> w = f / (1 + g*f)

Transfer function:

2 s^2 + 3 s + 1

-----------------------

2 s^3 + 5 s^2 + 5 s + 2

Этот результат может показаться неожиданным. Дело в том, что обе передаточных функции имеют первый порядок, то есть, описываются дифференциальным уравнением (ДУ) первого порядка. Поэтому вся система должны описываться второго порядка, а мы получили третий. Чтобы разобраться в этом, преобразуем модель к форме «нули-полюса»:

>> w_zpk = zpk(w)

Zero/pole/gain:

(s+1) (s+0.5)

-----------------------

(s+1) (s^2 + 1.5s + 1)

Видно, что числитель и знаменатель передаточной функции содержат общий множитель s+1, который можно сократить, и остается система второго порядка. Для этого надо построить минимальную реализацию, сократив общие множители:

>> w = minreal (w)

Transfer function:

s + 0.5

---------------

s^2 + 1.5 s + 1

Эта передаточная функция совпадает с той, что выдает функция feedback.

· контур с положительной обратной связью

>> w = feedback(f, -g)

или

>> w = feedback(f, g, 1)

или

>> w = minreal (f/(1 - g*f))

Transfer function:

2 s + 1

-----------

2 s^2 + 3 s

Корневой годограф

Многие важные свойства системы (например, быстродействие, перерегулирование) определяются расположением корней характеристического уравнения на комплексной плоскости.

Простейший способ коррекции системы – применить П-регулятор (усилитель с коэффициентом ), который изменяет коэффициент усиления разомкнутой системы и расположение этих корней. При изменении от 0 до корни описывают кривые, которые называются корневым годографом [11].

С помощью модуля SISOTool (сокращение SISO=Single Input Single Output обозначает систему с одним входом и одним выходом) можно выбирать нужное расположение корней (и соответствующий коэффициент усиления), «перетаскивая» их мышкой. Заметим, что при перемещении одного корня смещаются и все остальные, поскольку система имеет одну степень свободы – изменяющийся коэффициент усиления контура.

Корни при выбранном коэффициенте усиления изображаются фиолетовыми квадратиками. Концы годографа для каждого корня помещены крестиком () и кружком (). Сетка (для ее вывода надо нажать ПКМ на графике и выбрать пункт Grid) показывает линии равных показателей колебательности (коэффициента демпфирования, damping factor) – прямые, выходящие из начала координат, и линии равных собственных частот (natural frequency) – окружности с центром в начале координат.

В контекстном меню (ПКМ) можно установить ограничения на расположение полюсов так, чтобы перерегулирование и время переходного процесса не превышали заданных. Для этого надо выбрать пункт Design Constraints – New и выбрать в выпадающем списке Percent Overshoot (перерегулирование в процентах) или Settling Time (время переходного процесса с 2%-ной точностью). Ограничения показываются в виде границ запрещенных зон.

Время переходного процесса оценивается по степени устойчивости замкнутой системы. Так называется расстояние от самого правого корня характеристического уравнения до мнимой оси. Обычно принимается (как для апериодического звена)

,

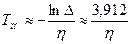где – величина допустимой ошибки (в Matlab она принимается равной 2% или 0,02). Таким образом, при ограничении только на область допустимого расположения корней есть полуплоскость .

Требования к коэффициенту демпфирования добавляют ограничение в виде сектора

.

Число называют колебательностью или степенью колебательности замкнутой системы. Каждому заданному соответствует некоторое значение .

Перерегулирование (в процентах) оценивается по формуле

.

Каждому перерегулированию соответствует свое значение 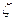и свой сектор, ограничивающий расположение корней.

Таким образом, при использовании двух ограничений (первое – на , второе – на или 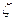) область допустимого расположения корней представляет собой усеченный сектор в левой части рисунка. Если перетаскиванием корней (то есть, изменением усиления контура) не удается расположить полюса в этой области, надо усложнять регулятор, добавляя его нули и полюса (ПКМ – Add Pole/Zero или ПКМ – Edit Compensator).

Не нашли, что искали? Воспользуйтесь поиском: