ФАКТОРНЫЕ МОДЕЛИ ИСПЫТАНИЙ

Коротко выделим основные типы используемых статисти­ческих комплексов. Прежде всего это планы полного фактор­ного эксперимента (ПФЭ), латинские, греко-латинские и гипергреко-латинские квадраты (см. 1.1.1), позволяющие про­изводить весь комплекс статистических вычислений по анали­зу исследуемого процесса.

Отметим, что внешние факторы могут быть как непрерыв­ными (влажность, температура и т. д.), так и дискретными. Примером дискретных факторов могут служить разные опера­торы, стенды или приборы, различные производственные пе­риоды, дни недели и т. п. Все они могут оказывать опреде­ленные непрогнозируемые воздействия на исход испытаний. В тех случаях, когда дискретные внешние переменные могут быть идентифицированы, т. е. оценены (случай активного экс­перимента) возможно применение рандомизированных планов испытаний типа латинского или греко-латинского квадратов (см. 1.1.1).

Во многих видах контрольно-испытательных работ рас­сматриваются два или более регулируемых переменных фак­торов (штатных параметров испытаний).

Последовательность проведения таких испытаний может составляться как в виде классической, так и факторной моде­лей (планов).

Классический план состоит в том, что все независимые переменные, кроме одной полагают постоянными (на одном определенном уровне), а одна изменяется по всем уровням в заданном интервале (например, фактор Y изменяется по всем 4-м уровням при наложении одного уровня внешней переменной «а»), В этом случае остальные клетки матрицы плана не заполняются.

По существу, классический многофакторный эксперимент представляет собой просто последовательность однофактор­ных экспериментов.

Если планируется классическая последовательность про­ведения испытаний (частичная или полная), то он не обяза­тельно должен быть сбалансированным. Это означает, что можно выбрать десять уровней переменной X и только три уровня переменной Y, если считается, что зависимость R от X — является боле важной или сложной. Например, при ис­пытаниях теплообменников часто рассматривается соотно­шение

St =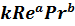

где число Стэнтона St — зависимая переменная, а число Рей­нольда Re и число Прандтля Pr — две независимые перемен­ные. В большинстве практически возможных случаев в ши­роком интервале температур число Рrа изменяется очень мед­ленно, а число , которое зависит от скорости потока жид­кости, может изменяться в широких пределах. При этом сле­дует варьировать числом Прандтля на значительно меньшем числе уровней, чем числом Рейнольдса [3].

Необходимо отметить, что применение факторных планов в контрольно-испытательных работах возможно в основном только в случае описания рабочих процессов двумя типами функциональных зависимостей. К первому типу относятся формулы, в которых зависимая переменная есть сумма функций от независимых переменных:

R= , (9)

где 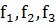функции любой сложности.

Но примеры такого класса независимо действующих соотно­шений факторов встречаются редко.

Ко второму типу, более часто встречаемому в практике, относятся соотношения, описываемые произведением отдель­ных функций независимых переменных:

(10)

Практически это частный случай зависимостей первого типа, т. к., логарифмируя (18), получим:

(11)

Последнее выражение одно из наиболее важных общих соотношений в технических работах. Оно включает результат, широко применяемый при анализе размерностей

(12)

а также множество различных сложных формул, например, таких, как:

(13)

(14)

Примеры функций, не относящихся к этому классу: R=AXa + YbZc; R=AXa +eBY|Z и др.

Если известен окончательный результат R и с помощью кривых или таблиц для переменных X, Y, Z можно определить отдельные значения R, то можно вычислить и К.

Основное преимущество многофакторных экспериментов при факторном планировании — более высокая точность, чем при классическом плане при таком же или несколько большем объеме испытания. Основным их недостатком является то, что выбор большого числа комбинаций условий, при которых затем проводится эксперимент, осуществляется при отсутст­вии данных о рабочей области. Другой недостаток — невоз­можность применения получаемых графиков без перехода к общим функциональным соотношениям.

В тех случаях, когда известно, что будет получена функ­ция 2-го типа соотношений, в которую входят несколько пере­менных, необходимо всегда применять факторный план.

Модификацией латинских квадратов являются комбинаци­онные квадраты планов испытаний [22]. Например, комбина­ционный квадрат для плана испытаний, содержащих 4 фак­тора на 5 уровнях, состоит из 52 = 25 средних квадратов, каж­дый из которых в свою очередь тоже разбит на 52 = 25 малых квадратов или «клеток». Таким образом, всего имеется 54 = = 625 клеток по полному числу сочетаний 4 влияющих фак­торов на 5 уровнях (см. табл. 18 или раздел 2.2). Эффектив­ность таких моделей тем больше, чем больше количество фак­торов. Их применение также ограничивается областью актив­ного эксперимента.

Часто при построении комбинационных квадратов об­наруживается такой недостаток — для некоторых его частей будет наблюдаться монотонное изменение нескольких факто­ров одновременно. Для устранения такого недостатка получен­ный комбинационный квадрат можно преобразовать путем перестановки столбцов и строк средних квадратов. При этом свойства ортогональности квадрата не меняются.

К разновидностям матриц ПФЭ можно отнести статисти­ческие комплексы Длина [9].

Первый основной тип комплексов (или планов) — «равноповторный» — характерен размещением значений выходного контролируемого параметра в клетках планов в равном коли­честве (схема плана типа табл. 1).

Статистические комплексы такого типа могут быть обра­ботаны методами факторного анализа лишь при наличии в каждой клетке не менее 2-х значений (правило минимальной двукратной повторности).

Если в клетках плана содержится разное количество зна­чений, но для каждого сочетания уровней по всей таблице сохраняется заданная пропорция относительно других сочета­ний, то такие планы называются пропорциональными. Причем в отдельных клетках может содержаться и по одному значе­нию. Равномерный и пропорциональный комплексы являются ортогональными (см. 1.2.1). К ним методы факторного анали­за применимы безоговорочно. В случае нарушения принципа пропорциональности распределения значений по клеткам таб­лицы, но при наличии в каждой клетке хотя бы одного значе­ния, такой план называется «неравномерным». Если в подоб­ном плане в отдельных клетках таблицы не окажется ни одно­го значения, то его можно назвать «неполным».

Неравномерные и неполные планы не являются ортого­нальными, поэтому здесь непригоден обычный факторный анализ, содержащий в основе дисперсионный анализ, а при­менимы, например, регрессионный и корреляционный ана­лизы.

Не нашли, что искали? Воспользуйтесь поиском: